
Specific systematic studies on the nuclear potential parameter for the heavy-ion reactions which includes the systems have been achieved by using large-angle quasi elastic scattering at deep sub-barrier energies close to the Coulomb barrier height. The elastic scattering barrier distribution \(D_{qel}\)as a function of energy has also been calculated in this theoretical study. The single-channel (SC) and coupled-channels calculations have been carried out to elicit the nuclear potential. The chi-square method \(X^{2}\) has been used find the best value of the nuclear potential in comparison with the experimental data. The best values of the nuclear potential were found from the calculations of the single channels for systems: \(^{16}O+^{166}ER\) , \(^{16}O+^{197}\)Au, which are equal to (60.5, 100) MeV, respectively.
Copyright © 2024 Ali A. Rakhees and Khalid S. Jassim. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The Coulomb barrier region offers a highly broad range of events in heavy ion collisions. The barrier splits as a result of different channels interfacing with one another [1], consequently, when compared to one-dimensional calculations, greatly raises the fusion cross sections in the sub-barrier region [2]. In nuclear physics, the tunneling phenomenon is shown by the fusion of two nuclei at extremely low energy. These processes not only play a crucial role in the synthesis of nucleic nucleosynthesis, and the creation of stellar energy, but they also shed fresh light on nuclear structure and reaction dynamics [3]. Heavy-ion fusion cross-sections may be replicated using a barrier penetration model at energy far higher than the Coulomb barrier. Combining the attractive short-range nuclear potential with the repulsive Coulomb and centrifugal potentials results in the one-dimensional fusion barrier [4].
Measured fusion cross-sections are commonly increased by calculations performed with this model for energy below this single barrier. It has long been understood and experimentally proven that static deformation effects can improve sub-barrier fusion. In this case, the amplification is caused by the dispersion of barrier heights, which may be understood as the result of different target nuclei’s distorted orientations [5]. Since penetration through the single barrier is substantially less likely than going over the smaller obstacles, the cross sections are boosted by any distribution of barriers around the single barrier, at energies lower than that of the single barrier [6].
A semi-classical model was used to examine the impact of surface vibrations collectively on fusion, which once more led to the dispersion of fusion barriers, even though crossing barriers whose heights are often lower than the fusion energy is what causes the majority of the cross sections [7]. The connection between separate reaction channels results in a dispersion of barriers instead of a single barrier [8]. The fusion barrier distribution, which incorporates the second derivative, may be used to conveniently study the sensitivity of fusion data to the coupling of distinct reaction channels. Furthermore, the potential parameters employed in theoretical calculations may be restricted by selecting a set of parameters that can duplicate the barrier distribution as precisely as feasible [9]. To get an accurate barrier distribution, very precise fusion cross sections must be measured [10].
Larger mistakes in the distribution extraction occur at energies slightly over the barrier when using the second derivative to derive the distribution. As an alternative, it was suggested that backward-angle quasi-elastic (QEL) scattering may produce a comparable distribution [11]. In general, scattering studies with heavy ions accelerated to varying energies and conducted on a variety of fixed targets have proven to be an helpful tool for learning more about the specifics of the interaction processes at as well as the characteristics of the nucleus itself, as demonstrated by the Geiger and Marsden experiments [12]. As a consequence, All interactions entail essentially the same information regarding the interaction mechanism and are subject to the same potential, both of which are vulnerable to channel coupling effects at energies near the colliding nucleus [13].
The couplings between motion and internal degrees of freedom in the colliding nuclei are primarily responsible for heavy-ion reactions at energies close to and below the Coulomb barrier [14]. One famous example is the rise in the sub-barrier fusion cross-sections relative to basic potential model predictions, which is attributed to strong couplings to mutual excitement [13]. For a number of heavy-ion systems, coupled-channel studies have been offered, accounting for particular coupling effects that fully explain quasi-elastic back angle scattering and experimental fusion interaction evidence [15]. The of this study is to obtain the nuclear potential parameters for the systems \(^{16}O+^{166}ER\) , \(^{16}O+^{197}\)Au by using large angle quasi-elastic scattering at deep sub-barrier energies close to the Coulomb barrier height, and the single channels and coupled-channels calculations were performed using the CQEL program, which includes all orders of coupling and is considered the most recent version of computer code CCFULL [16]. The best fitted values of the nuclear potential parameters in comparison with the experimental data have been obtained through the chi square method \(X^{2}\) [16]. Jassim and et.al have been studied quasi-elastic scattering for some heavy ion systems to find diffuseness parameters and some others important parameters [17, 18, 19, 20, 21].
Using the coupled channels technique, the nuclear structural impacts may be considered in a more quantal manner. To develop the coupled channels approach, consider a collision between two nuclei in the presence of the coupling of the relative motion \(r=(r , \hat{r})\) to a nuclear intrinsic motion \(\xi\). We assume the following Hamiltonian for this system [17, 22]: \[\label{e1}\tag{1} H\left(\mathop{r}\limits^{\rightharpoonup},\xi \right)=\frac{{\textrm{h}}^2}{2\textrm{µ}}{\mathrm{\nabla }}^2+V\left(r\right)+H_0\left(\xi \right)+V_{coup}\left(\mathop{r}\limits^{\rightharpoonup},\xi \right),\] where \(H_{o}(\xi)\) and \(V_{coup}(r.\xi)\),are the intrinsic and the coupling Hamiltonians, respectively. V(r) is the standard Woods-Saxon potential which has the form [17]: \[\label{e2}\tag{2} V_N\left(r\right)\mathrm{=-}\frac{V_0}{\mathrm{1+}{\mathrm{exp}} \left[\frac{r\mathrm{-}R_0}{a}\right]},\]
where \(a\) represents the diffuseness parameter. In general, the fundamental degree of freedom \(\xi\) has limited spin. Consequently, we raise the multipole coupling Hamiltonian [19]: \[\label{e3}\tag{3} V_{coup}\left(\mathop{r}\limits^{\rightharpoonup},\xi \right)=\sum_{\lambda >0,\mu }{f_{\lambda }\left(r\right)\ Y_{\lambda \mu }(\hat{r})\ T_{\lambda \textrm{µ}}(\xi )}.\]
Here Y\({}_{\mathrm{\lambda }\mathrm{\textrm{µ}}}(\hat{r})\) are the spherical harmonics and T\({}_{\mathrm{\lambda }\mathrm{\textrm{µ}}}\)(\(\xi\)) are spherical tensors built using the intrinsic coordinate system. The dot indicates a scalar product. The sum is taken over all except for \(\lambda\) = 0, this is already present in the bare potential, V(r). For a fixed total angular momentum J and its z-component M, the wave function’s expansion basis in Equation 2 is described as [19]. \[\label{e4}\tag{4} \left\langle \mathop{r}\limits^{\rightharpoonup}\xi \mathrel{\left|\vphantom{\mathop{r}\limits^{\rightharpoonup}\xi \left(nlI\right) JM}\right.}\left(nlI\right)\mathrel{\left|\vphantom{\mathop{r}\limits^{\rightharpoonup}\xi \left(nlI\right) JM}\right.}JM\right\rangle =\sum_{m_lm_I}{\left\langle lm_lIm_I\mathrel{\left|\vphantom{lm_lIm_I JM}\right.}JM\right\rangle }Y_{lm_l}\left(\hat{r}\right)\ {\varphi }_{n_Im_I}\left(\xi \right).\]
The intrinsic motion wave functions are subject to where \({\varphi }_{n_Im_I}\left(\xi \right)\) are the wave functions I ; l are the intrinsic and orbital angular momenta, respectively. [17, 23]: \[\label{e5}\tag{5} H_0\left(\xi \right)\ {\varphi }_{n_Im_I}\left(\xi \right)={\epsilon }_n{\varphi }_{n_Im_I}\ \left(\xi \right).\] In this context, stands for any quantum number beside angular momentum \(\alpha\). Using the channel wave functions, the overall wave function is amplified as [19]: \[\label{e6}\tag{6} \psi \left(\overrightarrow{r},\xi \right)=\sum_{n,l,I}{\frac{u^J_{nlI}\left(r\right)}{r}}\ \left\langle \overrightarrow{r}\xi \mathrel{\left|\vphantom{\overrightarrow{r}\xi (nlI) JM}\right.}(nlI)\mathrel{\left|\vphantom{\overrightarrow{r}\xi (nlI) JM}\right.}JM\right\rangle.\]
The equations for \(u^J_{nlI}\left(r\right)\ \)in the coupled channels are as follows [19, 23]: \[\label{e7}\tag{7} \left[-\frac{{\textrm{h}}^2}{2\mu }\frac{d^2}{dr^2}+V\left(r\right)+E+{\epsilon }_n\right]u^J_{nlI}\left(r\right)+\sum_{n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}}{V^J_{nlJ\textrm{;}n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}}\left(r\right)u^J_{n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}}}\left(r\right)=0.\]
In which the elements of the coupling matrix \(V^J_{nlJ\textrm{;}n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}}\left(r\right)\) are defined as [17]: \[V^J_{nlJ\textrm{;}n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}}\ \left(r\right)=\left\langle JM\left(nlI\right)\mathrel{\left|\vphantom{JM\left(nlI\right) V_{coup}\left(\mathop{r}\limits^{\rightharpoonup},\xi \right) \left(n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}\right)JM}\right.}V_{coup}\left(\mathop{r}\limits^{\rightharpoonup},\xi \right)\mathrel{\left|\vphantom{JM\left(nlI\right) V_{coup}\left(\mathop{r}\limits^{\rightharpoonup},\xi \right) \left(n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}\right)JM}\right.}\left(n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}\right)JM\right\rangle\] \[V^J_{nlJ\textrm{;}n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}}\ \left(r\right)=\sum_{\lambda }{{\left(-1\right)}^{I-I^{\textrm{´}}\ \mathrm{+}l^{\textrm{´}}\mathrm{+J}}f_{\lambda }\left(r\right)\left\langle l\left\|Y_{\lambda }\right\|l^{\textrm{´}}\right\rangle }\]
\[\left\langle nI\left\|T_{\lambda }\right\|n\ 'I'\ \right\rangle\]
\[\label{e8}\tag{8} \sqrt{\left(2l\ +\ 1\right)\left(2I\ +\ 1\right)}\left\{ \begin{array}{ccc} I^{\textrm{´}} & l^{\textrm{´}} & J \\ l & I & \lambda \end{array} \right\}\] Since the coefficient is independent of the coefficient M., as can be seen in the equation, it has been suppressed, and suppres the index J. After that, linked channels Eq. [e7] reads []: \[\label{e9}\tag{9} \left[-\frac{{\textrm{h}}^2}{2\mu }\frac{d^2}{dr^2}+V\left(r\right)+E+{\epsilon }_n\right]u^J_{nlI}\left(r\right)+\sum_{n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}}{V^J_{nlJ\textrm{;}n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}}\left(r\right)u^J_{n^{\textrm{´}}l^{\textrm{´}}I^{\textrm{´}}}}\left(r\right)=0\]
We may define the wave number, k\({}_{n}\)(r), by: \[\label{e10}\tag{10} k_n\left(r\right)=\sqrt{\frac{2\textrm{µ}}{{\textrm{h}}^2}\ \ \left( \begin{array}{c} E\ -{\in }_{nI}\ -\frac{{\textrm{h}}^2}{2\mu r^2}\ -\ V\left(r\right)- \\ v^J_{nlI\textrm{;}nlI}\left(r\right)\ \end{array} \right)}\] where \[\label{e11}\tag{11} k_n=\sqrt{\frac{2\textrm{µ}\left(E\ -\ {\ \epsilon }_n\right)}{{\textrm{h}}^2}}\] With that, we calculate the fusion cross section by[17]: \[\label{e12}\tag{12} {\sigma }_{fus}\left(E\right)=\frac{\pi }{K^2}\sum_J{\left(2J+1\right)P^J}\left(E\right)\] The distribution of fusion barriers is calculated by [17]: \[D_f\left(E\right)=\frac{d^2(E{\sigma }_{fus})}{dE^2}=\pi R^2_b\left[-\frac{d}{dE}\left[\frac{1}{1+{\mathrm{exp} \left[2\pi \frac{E-V_b}{h^2\omega }\right]\ }}\right]\right]\]
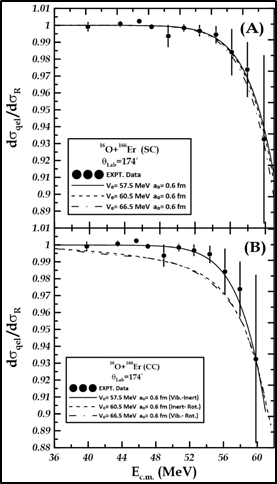
In \(^{16}O+^{166}ER\) system, We determined the nuclear potential parameter under conditions where both the projectile \(^{16}O\) and the target \(^{166}Er\) were considered to be single channel (SC) inert nuclei; as shown in Figure 1, with the nuclear potential’s parameter values \(V_{o}\)= (57.5,60.5,66.5) MeV respectively. In yet another instance, we assumed vibrational projectile \(^{16}O\) using a parameter for deformation \(\beta_{o}\)=0.358 to the a state \(2^{+}\)(6.917MeV) [24], with inert nucleus \(^{166}Er\), parameter value of the nuclear potential \(V_{o}\)=57.5MeV, the diffuseness \(a_{o}\) =0.6fm. In another case, the projectile \(^{16}O\) we suppose as inert nuclei, and considered target \(^{166}Er\) as rotational nucleus ; and a deformation a parameter \(\beta_{2}\)=0.285 and \(\beta_{4}\)= 0.007 [24], using a parameter’s diffuseness value \(a_{o}\) = 0.6fm, the nuclear potential \(V_{o}\) =60.5MeV , and the last event, we considered the target \(^{166}Er\) nucleus as nuclei of a rotational coupled with the projectile as vibrational nuclei \(^{16}O\) using a parameter for deformation \(\beta_{o}\)=0.358 to the state \(2^{+}\)( 6.917MeV ), value of the nuclear potential \(V_{o}\)= 66.5MeV , the radius parameter \(r_{o}\)=1.2fm and \(\theta_{Lab.}=174^\circ\).
| System | Case | $$r_o(fm)$$) | $$a_o(fm)$$) | $$V_o(MeV)$$) | $$\sigma_qel/\sigma R(X^2)$$) |
| 16O+166Er | Single channel | 1.2 | 0.6 | 57.5 | 0.00002 |
| 60.5 | 0.00001 | ||||
| 66.5 | 0.00011 | ||||
| Vib+Inert. Inert+Rot.Vib+Rot. | 1.2 | 0.6 | 57.5 | 0.00010 | |
| 60.5 | 0.00012 | ||||
| 66.5 | 0.00014 |
| System | Case | $$r_o(fm)$$) | $$a_o(fm)$$) | $$V_o(MeV)$$) | $$\sigma_qel/\sigma R(X^2)$$) |
| 16O+197Au | Single channel | 1.2 | 0.63 | 100 | 0.00001 |
| 115 | 0.00003 | ||||
| 125 | 0.00011 | ||||
| Vib.+Inert. Inert.+Rot. Vib.+Rot. | 1.2 | 0.63 | 100 | 0.00002 | |
| 115 | 0.00005 | ||||
| 125 | 0.00010 |
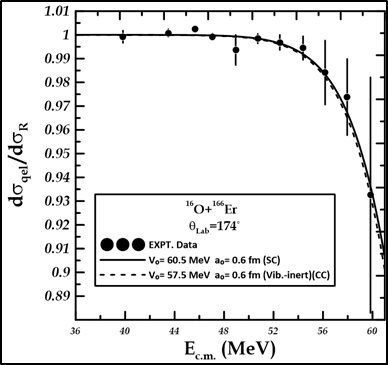
For \(^{16}O+^{166}ER\) system, the better-fitted nuclear potential parameter taken by measuring single channels is 60.5MeV, with \(X^{2}\) = 0.00001and \(a_{o}\) = 0.6fm. The dashed curve in (Figure 1) shows this. the good-match nuclear potential parameter, observed through a single-channel analysis, makes the experimental data a better fit than the one produced from a coupled channel analysis.
A comparison of the optimal values for the single channel and coupling channel, as determined by the chi-square \(X^{2}\) code, is shown in (Figure 2).
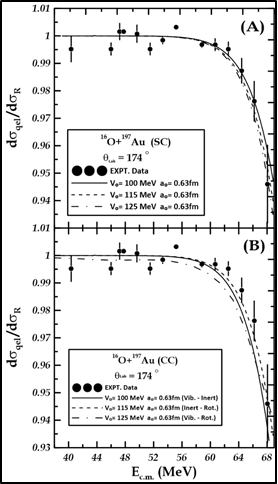
In \(^{16}O+^{197}\)Au system, we determined the nuclear potential parameter under conditions where both the projectile \(^{16}O\) and the target \(^{197}Au\) were considered to be single channel (SC) inert nuclei; as shown in (Figure 3), with the nuclear potential’s parameter values \(V_{o}\)= (100,115,125) MeV respectively. In yet another instance, we assumed vibrational projectile \(^{16}O\) with a deformation a parameter \(\beta_{o}\)=0.358 to the a state \(2^{+}\)(6.917MeV )[24], with inert nucleus \(^{197}Au\), parameter value of the nuclear a potential in this state \(V_{o}\)=100MeV, the diffuseness \(a_{o}\)=0.63fm. in the another case, the projectile \(^{16}O\) suppose as inert nuclei and considered target \(^{197}Au\) to be a rotational nucleus; and to have a deformation a parameter \(\beta_{2}\) = -0.125 and \(\beta_{4}\)=-0.017[24], using a parameter’s diffuseness value \(a_{o}\) = 0.63fm, the nuclear potential \(V_{o}\) = 115MeV , and the last event; we considered the target \(^{197}Au\) nucleus as a rotational coupling with the projectile as vibrational nuclei \(^{16}O\) value of the nuclear potential \(V_{o}\)=125MeV, the radius parameter \(r_{o}\)=1.2fm and \(\theta_{Lab.}=174^\circ\).
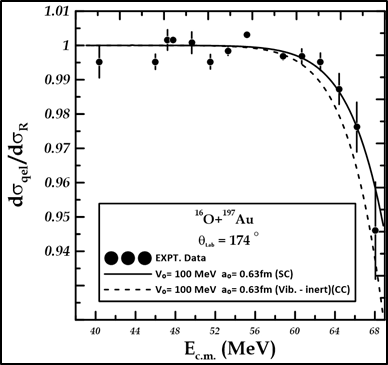
For \(^{16}O+^{197}\)Au system, the better-fitted nuclear potential parameter taken by measuring single-channels is 100MeV, with \(X^{2}\)=0.00001and \(a_{o}\) = 0.63fm. the solid curve in Figure 3 shows this. the good-match nuclear potential parameter, observed through a single-channel analysis, renders a better match for the experimental data than the result of a coupled-channel analysis.
A comparison of the optimal values for the single channel and coupling channel, as determined by the chi-square \(X^{2}\) code, is shown in Figure 4.
The method of large angle quasi-elastic scattering at deep sub barrier energies close to the Coulomb barrier height has shown to be a useful tool for examining the surface characteristics of inter-nucleus potential via precise and methodical analysis of the data. We note the correspondence between the theoretical calculations and the practical values in the graphs between the cross-section (\(d\sigma_{qel}/d\sigma_{R}\)) and the energy of the center of mass. It was found that the best values obtained using the chi-square method are from the single channels. As compared with the rotational coupling, the system’s vibration coupling was more successful in simulating experimental data and carrying out theoretical computations. We notice that the correspondence between practical and theoretical values often occurs in the region of low energies, and the cause this is that the region of low energies is under the coulomb potential barrier, which is the region in which the quasi-elastic scattering occurs.