
Fractal is a powerful tool for describing complex and irregular geometric objects in nature, and in order to obtain the ideal garden landscape effect, a garden landscape simulation system with virtual 3D visualization technology is designed. Reconstructs the Hologram terrain scene model by using the image feature points, selects the enclosing body hierarchy method to render the landscape scene elements by using OSG 3D graphic engine, and establishes the leaf information by using the Billboard model. Tree engine is used to achieve the loading and rendering of tree models in the landscape scene, and the rendered trees, water bodies and other element models are imported into the 3D terrain scene model. Select residential community as the experimental object, the system simulation results show that can obtain a better visual effect.
gardening design is based on garden planning, based on the theory of garden landscape design through scientific and artistic means to create a garden environment technology. Garden landscape design works need to be coordinated with the overall surrounding environment, to bring people the feeling of beauty [1]. District greening, road environment design, scenic area planning, etc. are garden landscape design, garden landscape design results need to provide convenience for human life, the design of artistry should be integrated with the geography of the cultural and regional characteristics, pay attention to the protection and use of natural resources, and promote the sustainable development of the ecological environment [2,3].
Landscape design method has gradually developed from the traditional two-dimensional to Hologram, how to comprehensively and truly present the details of the designed landscape is the difficulty of landscape design [4]. The result of the designed landscape is presented dynamically, which is conducive to the artistic creativity of landscape designers and facilitates customers to give their opinions on the designed landscape.
AutoCAD software appeared a large number of garden landscape planning software, but with a Hologram presentation of the effect of the technology class software is less [5]. Hologram through the Hologram reconstruction way of designing landscape, can make the design of the landscape in a better way to present [6,7]. The current mainstream Hologram technology can be analyzed by the hierarchical analysis method for qualitative and quantitative weighted decision-making [8]. where, the hierarchical structure of the hierarchical analysis method is the target layer, the criterion layer, the index evaluation layer of three levels, and its main evaluation steps are:
establishing the hierarchical structure → determining the judgement matrix → single sorting of the levels → total weight sorting of the three levels → weighting analysis.
The main consideration when using Hologram technology to evaluate the impact of landscape gardens is whether it is interactive and immersive [9]. According to the hierarchical analysis method, a hierarchical structure can be established to determine the judgement matrix and weights. The factors involved in the problem are divided into five levels to establish a multilevel hierarchical structure model [10].
When any two factors at the same level are compared in terms of importance, their importance is judged and quantified. When two factors belonging to the same level are compared on the basis of the criteria of the factors of the previous level, their relative importance is determined according to the evaluation scale, and a judgement matrix is constructed accordingly.
Calculate the eigenvectors of the judgement matrix, in order to determine the relative weights of the elements of each layer. Finally, through the calculation of the combined weights, the optimal plan is determined in accordance with the principle of maximum weight.
Among them, interaction, realism, diffusion, functionality and usage are the five main indicators of software evaluation, and their hierarchical ordering and relative weights are shown in Table 1
| Evaluate | Interactivity | Authenticity | Functionality | Usage degree | Extensibility | Relative weight | Hierarchical sorting |
| Interactivity | 1 | 7 | 6 | 8 | 8 | 0.583 | 1 |
| Authenticity | 1/7 | 1 | 4 | 6 | 5 | 0.212 | 2 |
| Functionality | 1/6 | 1/4 | 1 | 4 | 4 | 0.116 | 3 |
| Usage degree | 1/8 | 1/6 | 1/4 | 1 | 1 | 0.055 | 4 |
| Extensibility | 1/8 | 1/5 | 1/4 | 1 | 1 | 0.049 | 5 |
Natural landscapes are mainly composed of mountains, lakes, rivers, oceans, earth, trees, flowers, plants, clouds, smoke, fog and other natural geometric features. Since these landscapes are naturally occurring, their geometries are irregular, which makes it extremely difficult to simulate natural environments with computers in real-time realism. The rapid development of fractal theory provides an effective means for the simulation of natural landscape [11,12]. In this paper, based on the basic principles of Lindenmayer Systems, random midpoint displacement method and particle systems in fractals as theoretical basis, we analyze and study the current fractal modelling and simulation techniques for 3D modelling of plants, 3D terrain generation, as well as for natural landscapes such as clouds, smoke, fog, flames, forests, meadows and oceans [13].
The use of binocular vision stereo camera to establish a Hologram terrain scene of the landscape, the use of Sketch UP software to establish a Hologram tree model, all the required elements of the landscape design model to build the completion of the landscape design elements and the use of Unity3D engine will be completed the design of the garden scene to display to the user.
Virtual Hologram visual technology into the design of landscape simulation system, the system development process needs to be clear through the garden design unit of the different aspects of landscape design and functional requirements, based on the needs of landscape design system modules, so that the designed system has a high degree of practicality [14]. The overall structure of the designed virtual Hologram visual technology landscape simulation system is shown in Figure 1.

The designed system mainly consists of two parts: model scene design module and resource library. The model scene design module includes editing and model building two parts, the use of editing part of the system to achieve different operations editing, model building part of the system includes terrain modelling, tree modelling, water modelling and stone landscape modelling four parts, each part of the model building is completed through the rendering and animation part of the model built to achieve the integration of the integrated model, after the integration of the model that is, the final design of the garden landscape results [15]; Through the resource library to provide resource support for the system, the resource library, including garden library, plant picture library, garden plane symbol library, with the scene picture library four parts, the garden landscape design process needs to call the relevant resources, the use of file reading and writing module will be the resources converted to the required format, easy to access the system [16].
The binocular stereo vision camera is represented by \({l^T},{e^T},{v^T},{\omega ^T}\), denote the rotational quaternion, coordinate position, linear velocity and angular velocity of the camera, respectively, and the camera state equation can be obtained as follows:
\[\label{e1} {x_c} = {\left( {{l^T},{e^T},{v^T},{\omega ^T}} \right)^T}.\tag{1}\]
The 3D world coordinates of the camera map feature state vector using the feature points to form the camera map are \({g_i}{\left( {{x_i},{y_i},{z_i}} \right)^T}\).
\[\label{e2} x = {\left( {x_c^T,g_1^T,g_2^T,…,g_i^T,…,g_n^T} \right)^T},\tag{2}\]
\[\label{e3} \mathbf{x}_{\mathrm{c}, t+1}=\left[\begin{array}{c} e_{t+1} \\ l_{t+1} \\ v_{t+1} \\ \omega_{t+1} \end{array}\right]=\left[\begin{array}{c} e_t+\left(v_t+m_v\right) \Delta t \\ l_t \times l\left(\omega_t+m_\omega\right) \Delta t \\ v_t+m_v \\ \omega_t+m_\omega \end{array}\right],\tag{3}\] where \({\left[ {{m_v},{m_\omega }} \right]^{\text{T}}}\) denotes the process noise during the reconstruction of the 3D terrain scene.
The coordinates of the projected position of the random point \(Q\) within the reconstructed 3D terrain scene within the image are given in the following formula:
\[\label{e4} \left\{\begin{array}{l} x=\frac{g X_c}{Z_c} \\ y=\frac{g Y_c}{Z_c} \end{array}\right..\tag{4}\]
The coordinates of the observations in the captured image using feature points matching the map feature points are represented in the following equation:
\[\label{e5} D = {({D_1},{D_2}…{D_n})^T},\tag{5}\] where \(m\) and \({D_i} = ({u_i},{v_i})\) denote the number of matched feature points and the coordinates of the acquired image when the feature point is \(i\) , respectively.
Add the measurement noise \({u_i}\) to Eq.(5) to obtain the measurement equation as follows:
\[\label{e6} \mathbf{D}_i=\left[\begin{array}{l} u_i \\ v_i \end{array}\right]+\mu_i=\left[\begin{array}{l} \frac{g_u \times x_{i c}}{z_{i c}}+u_0 \\ \frac{g_v \times y_{i c}}{z_{i c}}+v_0 \end{array}\right]+\mu_i.\tag{6}\]
Style:
\[\label{e7} \left[\begin{array}{l} x_{i c} \\ y_{i c} \\ z_{i c} \end{array}\right]=K * \mathbf{X}^{\mathrm{W}}+t,\tag{7}\] where: \(({g_u},{g_v})\) and \(({u_o},{u_o})\) denote the focal length and optical, respectively; \(K,t\)denotes the external parameters; \({({x_{ic}},{y_{ic}},{z_{ic}})^T}\)and \({{\bf{X}}^{\text{W}}}\) denote the coordinates of the feature point in the binocular stereo vision camera coordinates and in the world coordinate system, respectively.
Based on the binocular stereo vision camera position \(({g_t},{l_t})\), the feature point position in world coordinates is initialized based on the 3D coordinates of the feature point in camera coordinates.
Setting \({e_{n + 1}}\) as the new feature point, the formula for the variance of this point under the camera can be obtained as follows:
\[\label{e8} {{\bf{Q}}_{{X_{{\text{RCGB}}}}}} = \left( {\theta _{{x_{{\text{R}}G\;{\text{B}}}}}^2,\theta _{{y_{{\text{RCCB}}}}}^2,\theta _{{z_{{\text{RCB}}}}}^2} \right),\tag{8}\]
\[\label{e9} {f_{n + 1}} = K\left( {{l_t}} \right){X_{{\text{RGB}}}} + {e_t},\tag{9}\] where: \({\theta _{{x_{{\text{RCB}}}}}},{\theta _{{y_{{\text{RCB}}}}}},{\theta _{{z_{{\text{RCGB}}}}}}\) denotes the standard deviation of the desired reconstructed scene in different directions within the binocular vision stereo camera coordinates; \(X\) and \(Q\) denote the state vector and covariance of the added feature point, respectively. It can be obtained that after adding this feature point, the binocular vision camera state of the reconstructed 3D terrain scene is transformed into:
\[\label{e10} Q^{\prime}=\left[\begin{array}{cc} Q & Q\left(\frac{\partial g_{n+1}}{\partial x}\right)^{\mathrm{T}} \\ \frac{\partial g_{n+1}}{\partial x} Q & \frac{\partial g_{n+1}}{\partial x} Q\left(\frac{\partial g_{n+1}}{\partial x}\right)^{\mathrm{T}}+\frac{\partial g_{n+1}}{\partial X_{\mathrm{RGB}}} Q X_{\mathrm{RGB}}\left(\frac{\partial g_{n+1}}{\partial X_{\mathrm{RGB}}}\right)^{\mathrm{T}} \end{array}\right] .\tag{10}\]
When the number of visible reconstructed point clouds from the binocular stereo vision camera is less than the total number of pixels2 3 during the 3D reconstruction of the terrain scene localization process, the external parameter \({T_{cw}} = \left[ {{K_{cw}},{t_{cw}}} \right]\) is used to set the 3D point clouds from the binocular vision camera within the world coordinates, so as to realize all the 3D reconstruction of the visible point clouds from the camera.
After reconstructing the terrain and environmental information of different elements within the scene need to be organized [17]. The enclosing body hierarchy method is selected, and the OSG 3D graphics engine is used to render the elements of the landscape scene [18].
The use of Sketch UP software can establish the material texture and transparency of the water body, but the use of the software for the dynamic water body by the light irradiation refraction and reflection must not be reflected, the need to use Sketch UP software to establish a static body of water first, through the animation software to achieve the water body of the refracted light and reflective light and other details, so that the establishment of the body of water model has a strong vividness and authenticity.
Landscape design contains a large number of tree models, if the sequential parameterization of trees, although the size of the advantages of precision, but the number of trees is too large, easy to cause the defects of the amount of data and rendering consumption is too large, the use of Tree engine can be achieved within the landscaping scene tree model loading and rendering [19].
The rendering process of loading the created tree model into the created 3D terrain scene model is shown in Figure 2.
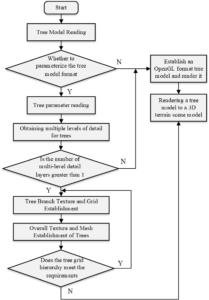
Read the created tree model into the tree engine, Parametric tree model format, obtain the number of tree multi-detail layers, when the number of multi-detail layers is greater than 1, establish the tree branches and trunks, the whole of the texture and mesh, and when the tree mesh layer meets the requirements of rendering, the completed rendering of the tree model will be imported into the Hologram terrain scene model.
Plants are living matter, the existence of randomness, singularity and complexity of the growth process, while the plant species are diverse, and the morphology of different species of plants is very different. These characteristics of plants should be fully considered in 3D modelling of plants [20].
The L-system, known as the regular grammar system, is a character parallel generalization of the plant growth process and abstract construction of axioms (representing plant seeds) and generative sets (describing the plant’s growth rules) . In order to build a complete and effective plant model, L-systems have been continuously extended with deterministic L-systems (D0L), stochastic L-systems, parametric stochastic L-systems, and context-dependent stochastic parametric L-systems. With the help of these L-systems, various morphologies of various plants and various characteristics during plant growth, such as plant pruning, plant phototropism and geotropism, are realistically modelled by constructing L-systems representing plant seeds and describing the growth rules of plants. As in Figure 3, plants generated by constructing different L-systems are shown, where (a) is a plant with normal morphology; (b) is the structure of a plant drawn after adding pruning factors to (a); (c) is a plant with normal morphology; (d) is the morphology change when the phototropic feature is obvious with respect to (c); (e) is the morphology change when the geotropic factor is large with respect to (c); and (f) is the structure of a plant with long flowers, fruits, and leaves.

Using the midpoint displacement method on a two-dimensional plane, called the 2D random midpoint displacement method, it is possible to simulate Hologram random fractal terrain using the 2D random midpoint displacement method. In this method, the core of the rectangle or square is displaced and the displaced height value is used as the new vertex, the rectangle or square is divided into four new rectangles or squares, the midpoint is then computed on each of the new rectangles or squares and the displacement is added to iterate repeatedly . As shown in Figure 4, the four corners were set to the same height, and the four corners of Figure 4 were given initial height values, indicated by black dots.
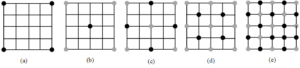
The computation at each step of the iteration can be summarized by the following equation:
\[\label{e11} {X_n}(x,y) = {f_n}(x,y) + {\Delta _n}*\operatorname{Gauss} ().\tag{11}\]
The offset added at each step is a random variable with a Gaussian distribution with variance: \(\Delta_{\mathrm{n}}^2=\left(\frac{1}{2}\right)^{\mathrm{nh}} \sigma^2\). Where \({X_n}(x,y)\) denotes the value of current point \((x,y)\), the location of viewpoint \((x,y)\), \({f_n}(x,y)\)denotes a Gaussian random number that follows a normal distribution. The shape of the mountain range with different roughness can be obtained by controlling \({\Delta _n}\).
The basic shape of the cloud can be defined as a simple ellipsoid then certain deformations are made to these cloud spheres in all different directions and the initial cloud sphere is randomly scaled down and randomly replicated several times at small displacements away from the of the cloud sphere in different orientations, continuing until the last iteration, and finally the scaled sphere is drawn [14]. In the modelling process, the fractal process is simplified and improved by treating the particles of the cloud directly as particles of the particle system, which has data information such as position, radius, color and transparency. The following discussion focuses on how to determine the position and radius of cloud particles using fractal techniques. The coordinates of the core of the cloud are \({\left( {X,Y,Z} \right)_{\text{ }}}\) , and the radius of the cloud is \(R\) . The position of the cloud particles offsets this core randomly, and its radius \(r\) is a number obtained by multiplying the distance to the core by a random interval that is [].Eq.(12) is the position formula and Eq.(13) is the radius formula. The base color of the cloud particles can be set to a uniform amount set to the color under no influence of light.
\[\label{e12} Cloun{d_i} \cdot {\text{X}} = {\text{X}} + {\text{R}} \times Randam(i),\tag{12}\] and the radius of the cloud particles can be expressed as:
\[\label{e13} {C_{{r_i}}} \ne {\text{R}} \times \Delta {{\text{L}}_{\text{i}}} \times {\text{R}}andom(i),\tag{13}\] where \(\Delta {{\text{L}}_{\text{i}}}\) denotes the distance of the cloud particle from the core of the cloud.
The fractal modelling process of the cloud is shown in Figure 5.

In order to give a realistic appearance to the cloud, the intensity of the color of the cloud ball is considered as a function of its height above the ground, with the color becoming more intense the closer the ball is to the ground, and gradually becoming lighter as the height increases.
When real-time simulation of clouds is achieved with a particle system, each particle represents a cloud mass, represented by a quadrilateral, mapping a 2D texture to a planar polygon and making that polygon always face the position of the observation point, thus creating a Hologram sense of a planar object, and generating a realistic sea of clouds through image synthesis and the multiple rendering technique in OpenGL. As in Figure 6.
Visual Studio 2010 is selected as the system development platform and is used as the development language to develop the system of this paper. Selected a city of a community landscape design as a system to verify the object, the community is located in the southeast of the city, is a newly developed ecological district, the district covers a total area of 13,854 m2, with a total construction area of 18,564 m2, the residential area contains a total of nine residential buildings, including villas, multilayer and high-rise areas, the landscape design requirements for the district greening area of more than 35%.
Hologram terrain scene modelling in landscape design is an important part of the landscape design contains numerous building information, with a large amount of modelling, the difficulty is high, selected binocular stereo vision camera used in this paper to establish the Hologram terrain scene model of the district as shown in Figure 7 . The Hologram terrain scene model established by the binocular stereo vision camera can include all the architectural information and road information of the landscape project to be reconstructed, and the reconstructed Hologram terrain scene model and the actual building can be presented at a ratio of 1:1, which is convenient for the designers to add the information of landscape elements in the future.

After the establishment of the Hologram terrain scene model, the need to establish the garden landscape related elements model, plant modelling is the difficulty of Hologram modelling of the landscape, plants contain leaves, branches and trunks and many other information, the establishment of the plant model can be as high as one million faces, and the garden design of the plants as the main elements, the use of this paper’s system to establish a Hologram tree model to the spruce tree as an example, this paper’s system establishes a Hologram spruce tree model shown in Figure 8 . Using the system in this paper can achieve the establishment of tree models within the landscape design scene, the establishment of the tree model has a high degree of fidelity, can reflect all the details of the tree information.

The model in this paper, shown in Figure 9, effectively establishes stone models in garden landscapes. Stones are vital in landscape composition, forming artistic paths and scenery. This system can create various stone shapes and materials, allowing the construction of extensive stone scenery.
Using the system in this paper for the community design landscape final effect diagram shown in Figure 10.


The system can design landscapes according to the specific characteristics of the experimental objects of the required landscaping design, which effectively reduces the labor intensity of the landscaping designers and shortens the design cycle. The garden landscape designed using the established 3D terrain scene model is more accurate than the 2D garden landscape design, and the accuracy of the garden landscape design is effectively enhanced because the 3D terrain scene model is established with 1:1 ratio. The system in this paper can design the landscape from a human point of view within the 3D scene model.
Hierarchical analysis method is selected to evaluate the effect of systematic design of garden landscape in this paper, hierarchical analysis method is a multi-objective decision analysis method combining quantitative and qualitative, which is extremely suitable for evaluation factors that cannot be quantified. The results of using hierarchical analysis to evaluate the garden landscape designed by the system in this paper are shown in Table 2. From the evaluation results in Table 2, it can be seen that using hierarchical analysis to evaluate the final effect of the garden landscape designed by this paper’s system through 10 indicators such as graphic refresh rate, visual brightness, visual contrast, etc., with an average score of 94.7, and the scoring results indicate that this paper’s system has a high degree of design effectiveness.
| Evaluating indicator | Weight | Evaluation results/points |
|---|---|---|
| Graph Refresh rate | 0.2346 | 96 |
| Visual Brightness | 0.0855 | 97 |
| Visual contrast | 0.0952 | 98 |
| Resolving power | 0.0864 | 92 |
| Stereo | 0.0576 | 93 |
| Shadow processing | 0.1686 | 94 |
| Illumination | 0.0829 | 95 |
| Special effects | 0.0716 | 94 |
| Model Scale | 0.0639 | 92 |
| Location correspondence | 0.0547 | 96 |
Fractal theory is one of the best tools to implement natural landscape simulation. Fractal recursive algorithms and L-systems are suitable for the simulation of virtual plants, fractional dimensional Brownian motion is suitable for Hologram terrain modelling, and particle systems are by far considered to be one of the most successful graphic generation methods for the simulation of irregular and dynamically changing objects, such as clouds, smoke, fog, flames, forests, meadows, oceans and so on. The virtual 3D vision technology is used to realize the simulation system design of the garden landscape, and the binocular stereo vision camera is applied to the 3D terrain scene reconstruction of the garden landscape design to enhance the immersion effect and realism of the system. The system successfully realizes the simulation of a community garden landscape, which verifies that the designed garden landscape has a high spatial utilization rate and fidelity, and the visual effect is good, and the colors within the garden landscape have a high degree of integration.
This work supported by R \& D Program of Beijing Municipal Education Commission (SM202210015003).