
With the rapid development of global electronic design automation (EDA) technology and the intensification of technological competition between China and the United States, the research on automatic layout algorithms for PCB (printed circuit board) modules has become particularly important. This article explores a new PCB module automatic layout algorithm based on deep reinforcement learning methods.Firstly, the challenges faced by PCB design and the limitations of existing algorithms were introduced. Then, two different state encoding methods were proposed: direct feature embedding and graph structure feature based. In the direct feature embedding method, the effective representation of the layout environment state is achieved by encoding the component feature information into different channels of the state matrix, as well as the layout area labeling method based on pin numbers. The method based on graph structure features utilizes the MLP model to extract node and edge information from the PCB circuit diagram, which is used as input for deep reinforcement learning neural networks to more comprehensively capture the complexity and connectivity of PCB layout. In addition, a deep reinforcement learning neural network structure suitable for different state encoding methods was designed, and the effectiveness and performance of the proposed algorithm were verified through experiments.The experimental results show that the PCB module automatic layout algorithm based on deep reinforcement learning has significant advantages in improving layout efficiency and optimizing design performance, providing new ideas and methods for promoting independent innovation in China’s EDA technology.
In recent years, global technological competition has become increasingly fierce, especially the technology war between China and the United States, which has attracted widespread attention [1]. As an important part of it, Electronic Design Automation (EDA) technology plays a crucial role in the modern electronics industry [2]. The United States has implemented a series of blockades and sanctions on China’s semiconductor industry under the pretext of national security, especially restricting Chinese companies from using advanced EDA tools. This not only seriously affects the development of China’s electronics industry, but also exacerbates the instability of the global semiconductor market [3,4].
EDA technology, as an advanced electronic design assistance technology based on computer and microelectronics technology, has experienced rapid development in the past few decades.However, the current global EDA market is still dominated by a few multinational companies (such as Cadence, Synopsys, and Siemens), which not only monopolize 77% of the global market share, but also occupy over 80% of the Chinese market share.In contrast, the development of EDA technology in China started relatively late and there is a significant gap with the international advanced level, especially in the early stages of the full process EDA design tools [5,6].
In this context, PCB (printed circuit board), as a key component of integrated circuit chips, its design and manufacturing quality directly affect the development of the entire electronic information industry [7]. With the development of electronic products towards miniaturization and density, traditional manual layout methods can no longer meet the needs of rapid development, especially when facing the challenges of complex circuits and high-density integration [8]. Therefore, researching efficient and fast PCB automatic layout algorithms has become one of the important topics in the current field of electronic design.
At present, the academic research on PCB automatic layout algorithms is still in the initial stage. Although some EDA tool companies have launched some commercial automatic layout tools, their universality and efficiency still have limitations [9]. In addition, existing automatic layout algorithms still face the optimization problem of layout results when dealing with complex PCB designs, such as insufficient comprehensive consideration of routing effects, PCB area, and power consumption optimization [10,11].
This article aims to explore a PCB module automatic layout algorithm based on deep reinforcement learning, and propose a new automatic layout method by combining computer graphics, mathematical optimization methods, and electronic manufacturing processes.Compared to traditional heuristic algorithms, deep reinforcement learning can optimize PCB layout schemes through large-scale data training and intelligent decision-making, improving design efficiency and performance. The research results of this article are expected to provide new ideas and methods for the independent development of EDA technology in China, and promote technological innovation and progress in the field of PCB design.
As shown in the PCB module layout algorithm framework based on deep reinforcement learning, a state encoder is set between the layout environment and the neural network. The function of this state encoder is to transform the actual layout state of the environment into an input state that is easy for the neural network to recognize [12].In deep reinforcement learning problems, the encoding of environmental states is crucial, and the quality of the encoding method directly determines whether the neural network can effectively recognize and distinguish environmental states, thereby affecting the accuracy of action Q-value prediction.In the PCB module layout problem, the layout environment is abstracted as an application program that executes layout actions, and the layout state refers to the combination of all component positions and angles. Components are the only role that constitutes the layout state [13]. Therefore, the encoding process from the environment state to the input state is actually the encoding process of component feature information.This article analyzes the packaging of components and obtains several component feature information as shown in Table 1. In order to encode these feature information into input states that are easy to recognize by deep reinforcement learning neural networks, this article explores two different state encoding methods.
| Index (Feature Index) | Feature |
|---|---|
| 1 | Width |
| 2 | Height |
| 3 | X coordinate |
| 4 | Y coordinate |
| 5 | Pins number |
| 6 | Orientation |
| 7 | Component type |
| 8 | Connected Pin ID |
The purpose of state encoding is to encode component feature information into an input form that is easy for neural networks to recognize. Neural networks often use tensors as inputs. In this paper, the PCB layout area is discretized into a 156×156 grid, which is stored in a 156×156 matrix in the computer. When components are placed on the layout area, the information in the corresponding grid area is essentially changed [11]. Therefore, this paper uses the discretization matrix as the carrier of component feature information, encodes it into a state matrix, and proposes a direct feature embedding state encoding method based on this.The so-called direct feature embedding refers to directly marking the corresponding layout area of a component in the state matrix as the feature value of that component.Each component has multiple features, and there are generally two ways to label multiple feature values [14]. The first method is to add different feature values and mark the added feature values in the corresponding layout area. This method can easily cause interference between different features and weaken the effect of certain features;The second method is to expand the feature matrix through channel expansion, setting different feature layers for each feature, and using channel superposition to expand the feature matrix. This article adopts the second method.
In addition to labeling the features of components, in order to increase the amount of information, this article uses the first layer of the feature matrix to label the laid out and non laid out areas. The existing layout algorithms usually use the “01” marking method to mark the layout area, which marks the non layout area as “0” and the layout area as “1”, as shown in Figure 1.
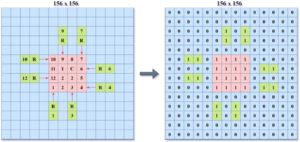
In the experimental process of this article, it was found that although the “01” labeling method is simple, it has a serious problem: this method will make all components show the same state in the state matrix, making it difficult for the network to recognize and distinguish different layout states.In fact, there is a direct or indirect connection relationship between peripheral components and core chips in PCB modules, which plays an important role in solving PCB module layout problems. In section 3 of this article, this connection relationship is used to divide layout areas and prioritize component layout.Therefore, when encoding the state, it is advisable to preserve this relationship as much as possible and increase the representation information of the layout state. Obviously, the “01” labeling method will lose this connection relationship. For this purpose, this article proposes a new layout area marking method called pin number based layout area marking method.
The layout area labeling method based on pin numbers refers to marking the corresponding layout area of the laid out components in the state matrix as the pin number of the core chip directly or indirectly connected to them, and also marking the pin area of the core chip as its pin number.As shown in Figure 2, assuming that component R1 is connected to pin 1 of the core chip IC22, the layout area corresponding to R1 is marked as pin number “1”, and the area corresponding to pin 1 of IC22 is also marked as pin code number “1”. Similarly, the layout areas of other components are also marked according to this method.For components indirectly connected to the core chip, use the “center diffusion method” proposed to search for the pin numbers of the core chip indirectly connected to it, and use the same method to mark them.

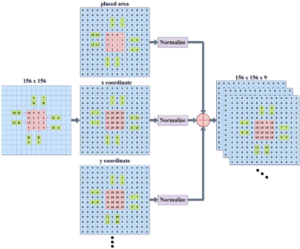
The layout area marker only encodes one channel of the state matrix, sets different feature channels for other features of the component, and sequentially encodes them into the state matrix. Each component has eight types of features, so a total of eight different feature channels need to be set. After stacking all feature channels, a feature matrix of \(156*156*9\) is finally obtained. The process of channel stacking is shown in Figure 3. For layout problems, certain features of components may be invalid, so the feature matrix may not be entirely composed of nine layers of channels. It is necessary to verify through experiments which combination of features is most effective.
In the DQN deep reinforcement learning framework, the gradient descent method is used to update the neural network. In order to prevent the network from being difficult to update due to excessively large eigenvalues, it is necessary to normalize the state matrix. There are generally two ways to normalize. The first is to add channels to the feature matrix and normalize it the same way. However, due to the different types of features in each layer and the different scales of feature values, this normalization method may reduce the expression ability of some small-scale feature information; Another approach is to first normalize each layer’s features separately, and then stack the feature channels. This article adopts the second normalization method.
Although the direct feature embedding state encoding method is relatively simple to implement, there are two key issues: first, the feature matrix is relatively sparse. To enable the neural network to extract effective feature information under sparse state inputs, a more complex neural network structure needs to be designed, which will increase the training difficulty of the network [16]. The second point is that PCB circuits are a natural graph structure, and for graph structures, in addition to node information that can serve as feature information, their connection information is also a very important feature information. In the direct feature embedding encoding method, although this paper proposes a layout area labeling method based on pin numbering to encode the connection relationship between components and their target pins, this encoding method cannot fully express the connection information of the circuit diagram structure. Therefore, this article starts with solving these two problems and proposes a state encoding method based on graph structure features.
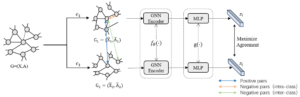
In PCB circuits, nodes can be represented by components or pins, and edges can be represented by the connection relationship between pins. The traditional approach to feature encoding through graph structure information is to use the node and edge information of the graph structure as inputs to train the graph convolutional neural network to fuse and extract the feature information of the graph structure. During the training process, information transmission is usually used to update the node and edge information of the graph.However, in order for graph convolutional neural networks to extract effective feature information, it is necessary to carefully design the neural network structure and information update method, and use a large amount of supervised information for training. To simplify the problem, this paper proposes a graph feature information extraction method based on the MLP model, which is much simpler compared to graph convolutional neural networks. Figure 4 is a schematic diagram of the model of this method.

In this feature extraction method, the pins corresponding to the components to be laid out are used as nodes, and information such as the length, width, pin coordinates, and number of the components are used as node information.
Two MLP models are set up in the network. The first MLP model is a feature extraction network, whose input is node information and edge information encoded by component features. The features are fused to extract useful feature information; The second MLP model is a prediction network that receives feature information extracted by the feature extraction network and predicts the corresponding layout line length.Using the true line length as the label information, the predicted line length is subtracted from the true line length, and the feature extraction network and line length prediction network are updated through backpropagation.After the model is stable, by inputting the graph structure information corresponding to the layout state, the model can predict a more accurate layout line length. At this time, the feature information extracted by the feature extraction network can effectively represent the layout state. Remove the line length prediction network, use the pre trained feature extraction network as the state encoder for deep reinforcement learning, encode the layout environment state, and use the encoded information as input for the deep reinforcement learning neural network [17].
As can be seen from the previous text, in the PCB module layout problem, the dimension of node information in the diagram structure is determined by the number of pins of the components in the circuit module. In the dataset, the number of components and pins in each circuit module is different, resulting in different dimensions of the corresponding node information matrix X and adjacency matrix, leading to different input dimensions of the network.In order to unify the input dimensions, a dimension transformation module is added before the feature extraction network to unify the graph information X from different dimensions into the same dimension input. The final network structure obtained is shown in Figure 5.
The goal of using deep reinforcement learning methods to solve PCB module layout problems is to train the optimal action value function, so that the function can accurately predict the Q values corresponding to each layout action under a given state of \(state\). At this point, selecting the action with the highest Q value to execute can optimize the layout state in a better direction. Therefore, the essence of the action value function is the mapping between the layout action and the Q value of the action under the specified layout state.In problems with lower state dimensions, the mapping relationship can be expressed in simple functions or table form. For example, in the Q-Learning algorithm, Q-Table is used to express the mapping relationship.The state space of PCB module layout problems is relatively large, and this approach cannot be adopted. It requires the powerful representation ability of neural networks to fit the action value function. Therefore, when using deep reinforcement learning to solve PCB module layout problems, the design of neural network structure is a crucial step.
The first form involves simultaneously inputting states and actions to predict the corresponding Q value;The second form is to only input the state and predict the Q value of all layout actions. Both input forms have their own advantages and disadvantages. The first input form can quickly obtain the Q value under specified states and actions, focusing on evaluating the value of individual actions, which can be more complex to implement; The second form focuses on comparing the Q values of all layout actions in the current layout state, which will be relatively simple to implement; However, for the problem of large action space, under this input form, the neural network needs to predict multiple action Q-values simultaneously, which will increase the network size and make training more difficult.Based on the previous analysis, it can be seen that in an inexperienced layout process, any component has \(156*156*4\) layout actions. If the second input form is used, each iteration of the neural network needs to predict the Q values of \(156*156*4\) actions simultaneously, which will make the fully connected layer parameters too large and cause training difficulties. Therefore, the first input form is adopted for this layout process.For the layout process guided by human experience, the number of actions corresponding to each component is uncertain. If the second input scheme is used, the output dimension of the neural network cannot be unified. Therefore, the first input form is also used for this layout process.
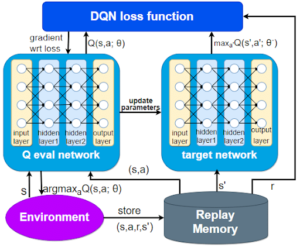
After determining the use of state and action combinations as inputs to the neural network, it is necessary to design corresponding neural network structures for different input sizes. This article proposes two different state encoding methods, corresponding to two different state inputs. Therefore, it is necessary to design two different neural network structures. Due to the many similarities between these two neural network structures, they are both represented by the schematic diagram of the neural network structure shown in Figure 6. From the figure, it can be seen that the neural network consists of four convolutional layers, a fully connected layer, and an output layer. The convolutional layer is used to extract feature information from the state action input, and multiple layers of convolution and different kernel sizes are set to extract feature information multiple times; The fully connected layer reduces the dimensionality of the high-dimensional features extracted by the convolutional layer, outputs the Q-value corresponding to the state action in the output layer, and uses a nonlinear ReLU activation function in the hidden layer.
The difference of neural networks under different state encoding methods is that the input state matrix is different. In the direct feature embedding encoding method, the components have a total of eight features, corresponding to the feature layers of eight channels, plus a feature layer used to mark the layout area, resulting in a total of nine feature channels. Therefore, under this encoding method, the size of the state matrix is \(156*156*9\), and the corresponding parameter information of each layer of the neural network is shown in Table 2.
| Hidden layer | Input | Convolutional kernel size | Step | Convolutional kernels | Activation function | Output |
|---|---|---|---|---|---|---|
| Conv1 | 156×156×11 | 8×8 | 4 | 32 | ReLU | 38×38×32 |
| Conv2 | 38×38×32 | 4×4 | 2 | 64 | ReLU | 18×18×64 |
| Conv3 | 18×18×64 | 3×3 | 2 | 128 | ReLU | 8×8×128 |
| Conv4 | 8×8×128 | 2×2 | 1 | 128 | ReLU | 7×7×128 |
| Fc5 | 7×7×128 | – | – | 512 | ReLU | 512 |
| Out | 512 | – | – | – | – | 1 |
Under the state encoding method based on graph structure features, the pre trained MLP feature extraction network is used to extract the graph structure feature information of the circuit, which is used as the state input of the deep reinforcement learning neural network. The feature matrix output by the MLP model is a tensor of size \(156*156*1\). Therefore, under this state input, the parameter information of the neural network is shown in Table 3.
| Hidden layer | Input | Convolutional kernel size | Step | Convolutional kernels | Activation function | Output |
|---|---|---|---|---|---|---|
| Conv1 | 156×156×11 | 8×8 | 4 | 16 | ReLU | 38×38×16 |
| Conv2 | 38×38×16 | 4×4 | 2 | 32 | ReLU | 18×18×32 |
| Conv3 | 18×18×32 | 3×3 | 2 | 64 | ReLU | 8×8×64 |
| Conv4 | 8×8×64 | 2×2 | 1 | 64 | ReLU | 7×7×64 |
| Fc5 | 7×7×64 | – | – | 512 | ReLU | 512 |
| Out | 512 | – | – | – | – | 1 |
By comparing the parameters shown in Table 2 and 3, it can be seen that the difference between deep reinforcement learning neural networks under the two different state encoding methods is the number of convolutional kernels, which is caused by the different number of input state channels.The main difference is that in the feature encoding method based on graph structure, the state input of deep reinforcement learning neural network is extracted through MLP model for feature extraction, which makes the feature information more effective and can better represent the layout status of PCB modules.
This chapter proposes a PCB module layout algorithm based on deep reinforcement learning and elaborates on the solutions to key problems in the algorithm. This section will verify the effectiveness of the solution through experiments. The experimental code is implemented in Python language and runs on a computer with the basic configuration shown in Table 4.
| Operating system | CPU information | Memory capacity | CPU information | CUDA Version |
|---|---|---|---|---|
| Debian11 | Intel(R)[email protected] | 64G | NVIDA A100-40G | CUDA 11.8 |
Under the framework of PCB module layout algorithm based on DQN, this paper first proposes the No Experience Process (NEP) and the Experience Process (EP) guided by manual experience;For the encoding problem from environmental state to input state, Direct State Encoder (DS) and Graph State Encoder (GS) based on graph structure features are proposed respectively. Two different layout processes and two different encoding methods are combined to obtain the following four different layout schemes:
Option 1: Empirically guided layout process+direct feature embedding state encoding, i.e. NEP+DS;
Option 2: Empirically guided layout process+graph structure feature state encoding, i.e. NEP+GS;
Option 3: Artificial experience guided layout process+direct feature embedding state encoding, i.e. EP+DS;
Option 4: Artificial experience guided layout process+graph structure feature state encoding, i.e. EP+GS;
In order to obtain the optimal layout strategy, this paper uses the PCB circuit module dataset proposed in section 2 to train models under four different layout schemes. As mentioned earlier, there are a total of 665 circuit modules in the dataset. In this section, 645 modules are used as training modules, and the remaining 20 modules are used as testing modules.Each layout scheme iteratively learns 100000 steps on each training module, obtaining four different layout strategies. The four layout strategies are used to layout 20 test modules, and the layout results are compared. In order to compare the algorithm in this chapter with traditional layout algorithms, this paper uses section 3 Artificial Empirical Method Assisted Genetic Algorithm (EGA) to layout 20 test modules iteratively for 2000.Under the framework of deep reinforcement learning, EP+DS and EP+GS layout schemes use the true value of line length, while NEP+DS and NEP+GS layout schemes use the estimated value of line length, and the EGA layout algorithm also uses the estimated value of line length. In order to ensure fairness in the comparison of results, Lee’s routing algorithm was used to route the final layout results of NEP+DS, NEP+GS, and EGA layout algorithms. The true values and pass rates of the routing were calculated and compared with the first two layout schemes.
When training deep reinforcement learning models, in order to balance the relationship between exploration and utilization, the \(\varepsilon\) greedy strategy is used to select layout actions.On the one hand, the layout action is randomly selected with a probability of \(\varepsilon\), so that the model can learn as much as possible the impact of selecting different layout actions in different layout states; On the other hand, using the network to predict the action with the maximum Q value with a probability of 1- \(\varepsilon\) allows the model to utilize the learned knowledge.The accuracy of the predicted values in the early stage of training is low, and learning should be explored as much as possible. In the later stage of training, the accuracy of the predicted values is high, and the learned knowledge should be utilized as much as possible. In order to accelerate the early learning and strengthen the later utilization, the initial value of the \(\varepsilon\) parameter is set to 0.9 in the experiment, and this parameter decreases with the increase of training times until it is fixed at 0.001, to ensure that the network converges as soon as possible in the later stage of training.
The learning rate of four different layout schemes in deep reinforcement learning is set to 0.00001. The NEP+DS and NEP+GS schemes use line length and area to construct rewards, with line length weight \({\omega _1}\)=0.5, area weight \({\omega _2}\)=0.5, line length discount parameter \({\gamma _1}\)=0.01, and area discount parameter \({\gamma _2}\)=0.0001; The EP+DS and EP+GS schemes use real line length to construct rewards, with a line length discount of \(\gamma\)=0.01. For artificial experience assisted genetic algorithms, the fitness function has a line length weight of \({\omega _1}\) for capacitors=1.0, a line length weight of \({\omega _2}\) for resistors=0.5, an area weight of \({\omega _1}\)=0.5, a line length discount of \({\gamma _1}\)=0.01, and an area discount of \({\gamma _2}\)=0.0001.The above five layout algorithms obtained various layout indicators under 20 test modules are shown in Table 5.
| Module Name | Number of devices | Layout algorithm | Deployment rate | Layout Line Length | Layout area |
|---|---|---|---|---|---|
| Block1 | 19 | NEP+DS | 0.88 | 3038.32 | 513493.66 |
| – | NEP+DS | 19 | 0.93 | 2682.99 | 495455.52 |
| – | EP+DS | 19 | 1.00 | 1884.37 | 340610.94 |
| – | EP+DS | 19 | 1.00 | 1088.41 | 340610.94 |
| – | EGA | 19 | 0.91 | 2293.13 | 479944.54 |
| Block2 | 19 | NEP+DS | 0.93 | 1943.34 | 509439.41 |
| Block2 | 19 | NEP+DS | 1.00 | 1665.46 | 486354.88 |
| Block2 | 19 | EP+DS | 0.98 | 1473.24 | 396354.54 |
| Block2 | 19 | EP+DS | 1.00 | 1389.12 | 396354.54 |
| Block2 | 19 | EGA | 1.00 | 1580.26 | 468822.42 |
| Block3 | 20 | NEP+DS | 1.00 | 1893.37 | 594733.41 |
| Block3 | 20 | NEP+DS | 1.00 | 1790.21 | 563322.52 |
| Block3 | 20 | EP+DS | 1.00 | 1405.66 | 354654.32 |
| Block3 | 20 | EP+DS | 1.00 | 1393.23 | 354654.32 |
| Block3 | 20 | EGA | 1.00 | 1477.35 | 404871.72 |
| Block4 | 20 | NEP+DS | 1.00 | 4016.83 | 587389.32 |
| Block4 | 20 | NEP+DS | 1.00 | 3927.36 | 544508.33 |
| Block4 | 20 | EP+DS | 1.00 | 2016.83 | 394508.80 |
| Block4 | 20 | EP+DS | 1.00 | 1654.34 | 394508.80 |
| Block4 | 20 | EGA | 0.86 | 3660.77 | 520266.46 |
| Block5 | 20 | NEP+DS | 0.67 | 4132.25 | 703839.85 |
| Block5 | 20 | NEP+DS | 0.78 | 3684.22 | 638394.26 |
| Block5 | 20 | EP+DS | 1.00 | 2154.45 | 394508.82 |
| Block5 | 20 | EP+DS | 1.00 | 1784.43 | 394508.80 |
| Block5 | 20 | EGA | 0.79 | 3379.37 | 615391.72 |
| Block6 | 21 | NEP+DS | 0.77 | 5028.54 | 729275.56 |
| Block6 | 21 | NEP+DS | 0.77 | 4872.21 | 706592.55 |
| Block6 | 21 | EP+DS | 0.85 | 3561.99 | 340610.94 |
| Block6 | 21 | EP+DS | 1.00 | 1302.96 | 340610.94 |
| Block6 | 21 | EGA | 0.83 | 4536.44 | 682341.92 |
| Block7 | 21 | NEP+DS | 0.79 | 14739.35 | 1939304.44 |
| Block7 | 21 | NEP+DS | 0.77 | 12928.32 | 1557439.32 |
| Block7 | 21 | EP+DS | 0.86 | 8344.56 | 850514.54 |
| Block7 | 21 | EP+DS | 1.00 | 4935.63 | 850514.54 |
| Block7 | 21 | EGA | 0.83 | 11031.43 | 1250688.53 |
| Block8 | 24 | NEP+DS | 0.79 | 14739.35 | 2103893.36 |
| Block8 | 24 | NEP+DS | 0.77 | 12948.36 | 1739473.49 |
| Block8 | 24 | EP+DS | 0.88 | 8344.56 | 1192655.46 |
| Block8 | 24 | EP+DS | 1.00 | 4935.63 | 1192655.46 |
| Block8 | 24 | EGA | 0.82 | 11031.43 | 1250688.52 |
| Block9 | 25 | NEP+DS | 0.79 | 10383.33 | 2103893.37 |
| Block9 | 25 | NEP+DS | 0.88 | 8247.32 | 1749473.29 |
| Block9 | 25 | EP+DS | 0.96 | 6362.13 | 1192655.44 |
| Block9 | 25 | EP+DS | 1.00 | 4722.15 | 1192655.44 |
| Block9 | 25 | EGA | 0.89 | 7934.06 | 1594169.35 |
| Block10 | 25 | NEP+DS | 0.63 | 20289.45 | 2294830.46 |
| Block10 | 25 | NEP+DS | 0.66 | 18363.56 | 2193840.57 |
| Block10 | 25 | EP+DS | 0.79 | 9639.33 | 1293094.43 |
| Block10 | 25 | EP+DS | 0.89 | 6072.46 | 1293094.43 |
| Block10 | 25 | EGA | 0.66 | 16817.55 | 1920459.95 |
From the above layout results, it can be seen that EP+DS, EP+GS, and EGA layout algorithms have better layout indicators than NEP+DS and NEP+GS layout algorithms in almost every test module. As mentioned earlier, the first three layout algorithms are all assisted by manual empirical layout methods, while the latter two layout algorithms are not assisted by manual empirical layout methods.This result once again confirms the conclusion of section 3 of this article, which is that the layout assistance method based on manual experience can indeed improve the layout quality of existing layout algorithms, and this method plays an important role in solving the layout problem of PCB circuit modules.
By comparing the layout results of NEP+DS and NEP+GS algorithms, as well as the layout results of EP+DS and EP+GS algorithms, it can be seen that under the same layout process, using the state encoding method based on graph structure features yields better layout results than using the state encoding method directly embedded with features.This indicates that under the state encoding method based on graph structure features, adding connection information of components in PCB circuit modules can indeed increase the richness of feature information, making state encoding more effective in representing layout states.At the same time, due to the need to train an MLP model to extract graph structure feature information under this state encoding method, this result also indirectly verifies the effectiveness of the pre trained MLP model.
In order to visually compare the differences in layout results between different algorithms, this paper selected a typical PCB testing module and visualized its layout or routing results obtained under different layout algorithms.Figure 7 shows the layout results obtained using random methods.The line length index uses estimated values, and from a quantitative perspective, their layout quality is relatively poor compared to the other two schemes. Therefore, their routing results are not evaluated during visualization.

Figure 7 shows the random layout results, which can also be seen as the initial layout states of the NEP+DS scheme, NEP+GS scheme, and EGA algorithm.Initially, the components were placed in a more scattered and disorderly manner. Under the optimization of the algorithm, the components gradually approached the core chip and became closer to their target pins, resulting in a smaller layout area and a significant improvement in line length and area indicators. This indicates that the algorithm can indeed play a role in optimizing the layout.Further comparison shows that compared to the other two layout schemes, the EGA algorithm, with the assistance of manual experiential layout methods, has a higher degree of component aggregation and better layout indicators in the visualization results, verifying the effectiveness of manual experiential layout assistance methods.
As mentioned earlier, in the state encoding method based on graph structure features, the first step is to fuse and extract the graph structure feature information of the layout state through an MLP model. Then, the extracted feature information is fed into the line length prediction MLP model to predict the routing length under this layout state. The true line length is used as the label information, and the loss is calculated with the predicted line length. The gradient descent method is used to update the feature extraction MLP model and the line length prediction MLP model simultaneously.Training this network requires a large amount of sample data. Therefore, in section 2, based on the PCB module dataset, this paper generated a large amount of data with layout status as samples and routing length as labels.
During the network training process, Adam is used as the optimizer and Mean Square Error (MSE) is used as the loss function. Assuming that the actual wiring length is \(y\) and the predicted wiring length by the model is \(\hat y\), the loss function is shown in Eq. 1.
\[\label{e1} \operatorname{Loss}(\hat{y}, \hat{y})=\frac{1}{n} \sum_{i=1}^n\left(y_i-\hat{-} y_i\right)^2.\tag{1}\]
Set the Batch Size to 64 and the learning rate to 0.00001. Train 2000 iterations on the dataset, and the resulting loss curve is shown in Figure 8. From the figure, it can be seen that the training loss and testing loss gradually converge to zero when the model iterates approximately 1500 times, indicating that the model can predict a more accurate routing length under the specified layout state. As the routing length is an important reflection of the layout state, it is clear that the model can effectively identify different layout states and extract feature information that effectively represents the layout state.

This article explores a new PCB module automatic layout algorithm based on deep reinforcement learning technology, and verifies its effectiveness and performance in experiments. By comparing traditional methods with proposed algorithms, the new algorithm exhibits significant advantages in layout efficiency and design performance.Specifically, we have designed two different state encoding methods and achieved effective representation of layout environment states: one is to encode component feature information into different channels of the state matrix through direct feature embedding, and the other is based on graph structure features to extract node and edge information from the circuit diagram using the MLP model.These state encoding methods not only improve the algorithm’s understanding of PCB layout complexity, but also enhance the algorithm’s adaptability and generalization ability. The experimental results have verified the superiority of the proposed algorithm in terms of layout efficiency and design quality, especially in dealing with large-scale PCB layout problems. Compared with traditional methods, the new algorithm has shown significant advantages in reducing wiring length, reducing power consumption, and improving signal integrity.
Future research can further explore how to combine more advanced deep learning technologies, such as graph neural networks and reinforcement learning, to further improve the efficiency and performance of PCB layout algorithms. At the same time, practical applications and optimizations in different application scenarios can also be considered to meet the needs and challenges of different electronic product designs.