
College education has gradually become one of the objects that our country attaches great importance to. Chorus teaching itself has strong practical characteristics, which requires teachers to change their original ideas, constantly explore new teaching methods, and combine theory and practice as much as possible, so that music majors can develop in an all-round way in conducting. Compared with the traditional non-statistical algorithm, the algorithm proposed in this paper borrows the statistical framework and model in continuous speech recognition, and has better robustness. In terms of acoustic model, high-order cepstral coefficients are used as features to avoid the negative impact of turbidity judgment and fundamental frequency estimation errors on system performance. At the same time, a key-independent quaternion model is trained to reflect the musical prior knowledge. The melody recognition result is finally obtained by the Viterbi decoding algorithm. Experiments show that the proposed algorithm has the best robustness under noisy conditions, while the performance on clean data is close to the best results among all the compared systems. On the basis of expounding the current situation of chorus conducting teaching in colleges and universities, this paper analyzes the innovative ideas of choral conducting teaching in the new media environment, in order to provide a reference for the teaching mode of choral conducting in colleges and universities.
Home teachers have attempted to integrate the Internet and new media technology into the classroom [1,2], but a systematic teaching system has yet to be established. On the one hand, new media teaching facilities in colleges and universities are not fully widespread, and many institutions lack new media teaching equipment and promotion platforms, leaving them in an exploratory phase. Therefore, college teachers should fully utilize the resources and platforms available in the new media era, incorporate new technologies into classroom teaching, explore modern models of chorus conducting instruction, and seek more effective methods for enhancing teaching outcomes and fostering greater innovation [3,4].
In the context of conducting education in colleges and universities, the rhythm of the entire activity is highly dynamic, necessitating the integration of transitional links [5]. This enhances the overall effect and provides the audience with a better experience [6]. The relationship between the chorus and the conductor is very close, and they are mutually dependent. However, some teachers have a superficial understanding of the music conducting course, focusing solely on explaining conducting techniques without addressing the broader aspects of conducting from a choral perspective. This gap in understanding affects the effectiveness of teaching [7,8].
When teaching conducting, educators should continually innovate their teaching methods to ensure high-quality instruction [9]. However, some teachers still rely on traditional teaching models, which makes student learning passive and results in a dull classroom atmosphere, ultimately leading to poor teaching outcomes.
For music majors, rhythm is a crucial element [10,11]. Teachers should therefore prioritize this aspect and enhance students’ sense of musical rhythm through targeted training methods. By encouraging students to understand musical rhythm through physical movement, they can quickly grasp the rhythm and contribute to a more cohesive choral performance [12]. Chorus conductors must possess a strong ability to appreciate music, allowing them to capture the essence of a piece during a performance and creatively reinterpret it to enhance the overall appeal and impact of the performance [13]. Therefore, developing students’ musical appreciation skills is also essential [14]. For example, teachers can regularly expose students to diverse musical pieces to enhance their appreciation abilities.
Chorus melody recognition involves identifying the sequence of notes from a choral signal and is primarily used as the front end of a chorus query system [15]. Many current chorus recognition systems need to analyze the note sequence in the choral signal for melody matching [16]. Thus, the accuracy of melody recognition directly impacts the performance of the chorus query system. Other applications of melody recognition include the convenient input of MIDI music without electronic music input devices and for karaoke scoring systems.
Most existing chorus melody recognition algorithms are based on non-statistical methods [17], utilizing signal processing-based fundamental frequency extraction algorithms and various note segmentation processes. These methods often lack robustness to different speakers and noisy environments. Consequently, some researchers have explored statistical models for melody recognition. [18] proposed a two-stage statistical recognition algorithm. First, note segmentation is performed using a hidden Markov model trained on MFCC features, dividing the choral signal into segments labeled as “note” or “silence.” Then, each segment’s pitch is labeled using a Gaussian mixture model trained on fundamental frequency features. To ensure accurate note segmentation, this algorithm assumes that the choral signal contains only certain syllables, such as “da” or “ta.” The melody recognition algorithm proposed by [19] and [20] integrates a hidden Markov-based pitch trajectory model and a binary grammar-based music model, assuming the known tempo of the chorus melody.
The algorithm proposed in this paper draws on probabilistic frameworks and models from advanced continuous speech recognition systems. Each note (and silence) is treated as a separate word in the algorithm. When training the acoustic model, high-order cepstral coefficients are used as features, which avoids rigid decisions regarding voicing and fundamental frequency estimation, reducing the negative impact of these errors on system performance. Simultaneously, a key-independent quaternary language model is trained to reflect the prior probability distribution of different note sequences in the song. Finally, the melody recognition results are obtained using the Viterbi global search algorithm.
In a continuous speech recognition system, let \(X = X_1 X_2 \cdots X_n\) represent the speech feature sequence. The word sequence \(\hat{W} = w_1 w_2 \cdots w_m\) output by the system maximizes the posterior probability \(P(W \mid X)\), which can be expressed as:
\[\label{e1} \hat{W} = \mathop{\arg \max}\limits_W P(W\mid X) = \mathop{\arg \max}\limits_W \frac{P(W)P(X\mid W)}{P(X)}.\tag{1}\]
To apply continuous speech recognition technology to melody recognition, the word sequence can be interpreted as a sequence of notes. By training the corresponding acoustic model and language model, the melody recognition result can be obtained using the continuous speech recognition framework.
Most existing melody recognition systems use the fundamental frequency as a feature. Although there is a direct relationship between fundamental frequency characteristics and note pitch, errors in fundamental frequency estimation (and voicing determination) cannot be avoided, even with advanced algorithms. In a noisy environment, this issue becomes more pronounced. If the fundamental frequency is used as a feature, errors in its estimation will negatively impact the melody recognition results. Therefore, to improve robustness, this paper adopts high-order cepstral coefficients as acoustic features.
Figure 1 shows the cepstral features of a frame of a signal with a pitch of middle C (C4) and a frame of silent signals, respectively. For clarity, the low-order part of the cepstrum, unrelated to fundamental frequency information, has been filtered out.
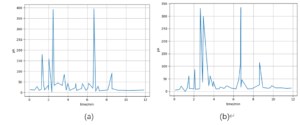
The sampling rate is 16 kHz. It can be seen from Figure 1 that there are obvious peaks in the cepstrum of the voiced signal, while the cepstrum of the silent signal is relatively flat. The order lag \(N\) of the cepstrum and its corresponding frequency have the following relationship: \(\operatorname{lag} N \times f(\operatorname{lag} N) = \text{sample rate}\).
The cepstral features shown in Figure 1 are processed as follows before being used to train acoustic features. First, the portion corresponding to the fundamental frequency range of the human voice is cut from the entire cepstrum. In the experiments, for male voices, this ranged from lag \(N = 48\) to lag \(N = 240\) (sampling rate 16 kHz), corresponding to the pitch range of C2 to E4 on a piano keyboard; for female voices, this ranged from lag \(N = 24\) to lag \(N = 120\), corresponding to the pitch range of C3 to E5 on a piano keyboard. Then, the cut-out cepstrum part is normalized to a fixed length by averaging the cepstrum values of adjacent orders. In the experiments, this fixed length is 24. It should be noted that in this process, the male voice cepstrum signal is compressed twice as much as the female voice signal, which is equivalent to doubling the fundamental frequency value contained in the male voice signal.
In the experiments, the data used to train the acoustic model consisted of three speakers (two male and one female). The data for each speaker includes two types: Type 1 contains choruses with the syllable ’da’, and Type 2 contains lyrics. The total amount of Type 1 data is about 45 minutes, while the total amount of Type 2 data is about 1 hour. Data was recorded in an office environment with a sample rate of 16 kHz. All chorus data is labeled as a semitone on the piano keyboard based on the actual pitch of the notes.
Each semitone (and silence) between E3 and D5 corresponds to an HMM. Each HMM model contains three states, and the probability density function of each state is modeled by a GMM. Similar to the acoustic model training process for continuous speech recognition, all HMM models are simultaneously trained using the forward-backward algorithm. Figure 2 shows the mean vector of all state GMM models in the C4 and C5 two-note HMM models after training.

In music theory, each key contains seven notes, and each octave consists of twelve semitones. This means the probability of a note appearing in a song is not uniform; instead, there is a distribution of prior probabilities. Therefore, language models are trained on prior distributions of note sequences for melody recognition.
The training data for the language model comes from the EsAC database and includes 522 melodies. The language model training in our experiments is tone-independent. First, all melodies are normalized to the same key, then transposed to the other eleven keys, and finally combined to form a large database for training the language model. The advantage of this approach is that it eliminates the need to explicitly determine the key of the chorus melody. After experimental comparison, a quaternary language model was selected.
To evaluate the melody recognition results in terms of the overall performance of the chorus query system, we developed a chorus query baseline system. The system converts both the melody and chorus query signals in the melody library into note sequences and then performs matching based on these sequences. Finally, a list of matching melodies is generated.
Since the melody and chorus melodies in the melody library may be in different keys, the notes are expressed as relative pitches during melody matching, representing the difference between the pitches of two adjacent notes. In the current baseline system, the duration information of notes is not used. The melody matching process can be divided into three steps: (1) Fast matching, where possible candidate matching points are quickly identified based on the index of the n-gram note sequence; (2) Coarse matching, which uses a string matching algorithm with lower complexity to narrow down the range of candidate matching melodies; (3) Fine matching, which uses a dynamic programming algorithm to determine the final melody matching result.
In fast matching, the melodies in the melody library are indexed in advance according to the sequence of n-grams (relative pitch). Upon matching, the index is retrieved based on the relative pitch sequence contained in the chorus melody. Since errors may be present in the recognition results, this paper adopts a fuzzy matching strategy to expand the sequence of notes identified from the chorus signal into a network, as shown in Figure 3. Each node represents a note output by the melody recognition algorithm, and the edge between two nodes represents the relative pitch between the notes. In addition to the relative pitch obtained directly from the melody recognition results, a relative pitch differing by one semitone is also added to the network. All relative pitch sequences contained in the network are used to retrieve the index.
The candidate matching points returned by fast matching are represented as ternary vectors \(Qk P\), where \(P\) is the starting position of the n-gram sequence in the chorus melody network, and \(k\) and \(Q\) are the starting positions of the corresponding n-gram sequence in the candidate melody and the serial number of the melody in the melody library, respectively.
When determining the value of \(n\), if the value is too small, the number of candidate matching points returned by fast matching may be too large, and the matching range cannot be effectively narrowed down. Conversely, if the value is too large, the amount of information contained in the n-gram sequence is relatively large, which can narrow down the matching range effectively, but the recall of fast matching will drop due to possible errors in the melody recognition. Through experiments, this paper sets the value of \(n\) to 4 (4 notes, which means 3 relative pitches). The melody library used in the experiment includes 1325 melodies.
Both coarse matching and fine matching use string matching algorithms. A low-complexity algorithm is used in the coarse matching stage. Let \({a_1}{a_2} \cdots {a_m}\) be the relative pitch sequence identified from the chorus signal, and \({b_1}{b_2} \cdots {b_n}\) the relative pitch sequence contained in the candidate melody. If it is assumed that at a certain point in the matching process, \({a_i}\) matches \({b_j}\), denoted as \({p_{ij}}\), then the next matching point in the matching path is:
\[\label{e2} \operatorname{Next}(p)=\arg \min \left\{\begin{array}{l} d\left(a_{i+1}, b_{j+1}\right) \\ d\left(a_i, b_{j+1}\right)+d\left(\phi, b_{j+1}\right) \\ d\left(a_{i+1}, b_j\right)+d\left(a_{i+1}, \phi\right) \end{array}\right.\tag{2}\]
Compared with the dynamic time warping (DTW) algorithm, this algorithm retains only one path in the matching process, making it more efficient than the DTW algorithm. After calculating the coarse matching cost of all candidate matching points returned by fast matching, they are sorted, and the top \(N\) candidate matching points are returned to the fine matching module.
The fine matching module adopts the DTW algorithm. The algorithm calculates the cost matrix \({D_{0 \ldots m,0 \ldots n}}\) with initial conditions:
\[\label{e3} \begin{cases}{D_{0,0}} = 0,\ {D_{0,j}} \\ {D_{0,0}}= \text{INF for } 1 \leqslant j \leqslant n,\ {D_{i,0}} \\ {D_{0,0}}= \text{INF for } 1 \leqslant i \leqslant m. \end{cases}\tag{3}\]
On the test platform, performance test experiments were conducted to evaluate the calculation of edit distance, DTW, and OSCM methods across five cases, with data volumes of 4,500, 9,000, 18,000, 36,000, and 72,000 songs, respectively. Simulated tests with 1,500 queries containing 3 random errors were also performed.
Since the OSCM algorithm allows for user-selectable parameters, this section explores the effects of different parameter selections on the algorithm’s performance.
In the OSCM algorithm, the database uses the binary code of each segment as the hash code for the melody contour index. The length \(n\) of the feature segment significantly impacts the algorithm’s performance. A larger \(n\), i.e., a longer segment, results in fewer records in the database corresponding to the index item of that segment, yielding fewer intermediate results from the query and thus faster query speeds. The experimental results shown in Figure 4 confirm this expectation.
The value of \(n\) also affects the error tolerance of the algorithm. If the input has no errors, or contains errors consistent with the melody contour, the algorithm’s top 3 hit rate is 100%. If the input contains errors opposite to the melody contour, the algorithm demonstrates good fault tolerance. According to the calculation method of one-sided continuous matching, the hit rate for the top 3 results will still be high. However, if the input includes two or more errors in the opposite direction of the melody contour, these errors significantly impact the algorithm’s hit rate. If the distance between two adjacent errors in the opposite direction to the melody contour is less than \(n\), the algorithm calculates low similarity, resulting in a lower hit rate. According to the user chorus error model in [], the distance between two adjacent user chorus errors that are opposite to the melody contour is generally greater than 4. Therefore, when \(n\) is 3, the algorithm should exhibit good fault tolerance. The cases where \(n\) is 3, 4, and 5 were selected for testing. As shown in Figure 5, when \(n=3\), the hit rate of the initial query, with varying data volumes, is 15%-20% higher than that of the top 10 queries with \(n=5\).


In the OSCM algorithm, the number of levels of the melody contour feature value also has a significant impact on the performance of the algorithm. When the number of levels is large, the number of records corresponding to each segment index item decreases, leading to fewer intermediate results from the query and thus faster query speeds. The experimental results shown in Figure 6 are consistent with this analysis. When the database contains 72,000 songs, the query response time using the 3-level melody contour method is approximately 2.5 times faster than that using the 5-level melody contour method.
Similarly, an increase in the number of levels results in a more accurate representation of the query input, which improves the query hit rate. Additionally, since the feature representation remains a melody contour, it retains good fault tolerance. The experimental results shown in Figure 7 demonstrate that the query hit rate of the algorithm varies with the number of pieces in the music database for different melody contour classification strategies. It can be observed that when the 5-level melody contour classification strategy is employed, the top 10 hit rate of the query algorithm is about 20% higher compared to when the 3-level melody contour classification strategy is used.

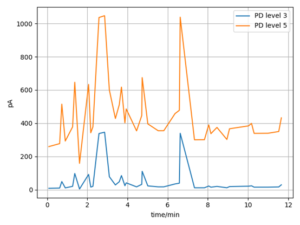
In the OSCM algorithms involved in the comparison, n is 3, and the melody contour adopts a 5-level classification strategy. Figure 7 shows the top 3 query hit rates of the three algorithms under different data sets. Figure 8 shows the three algorithms in different The top 10 query hit rates under the dataset.
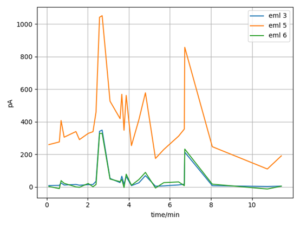
As shown in Figures 7 and 8, among the three algorithms, the DIW algorithm has the highest top 3 and top 10 query hit rates. When the number of songs in the database increases, the query hit rate of the DTW algorithm decreases the slowest. The hit rate of the query is nearly the same for data volumes of 18,000 and 72,000, and similarly, the data volume does not significantly affect the hit rate between 36,000 and 72,000. This indicates that the DTW algorithm has the best scalability among the three algorithms.
Generally, students’ emotional fluctuations are significant, but their rational thinking improves with age. Teachers can leverage this characteristic by adapting their teaching methods to the age and personality traits of students to stimulate their interest in learning. Common strategies include psychological effects and rhythm teaching. For instance, if students show a lack of interest in music lessons and prefer to sleep during class, teachers can guide them to study outdoors and experience nature in local parks. Teachers can also participate in these activities, which can greatly relax students, improve relationships with teachers, and encourage the sharing of views and opinions, thereby enhancing their overall ability.
Considering the query hit rate and query speed, the OSCM algorithm is deemed the best among the three algorithms.
Currently, many teachers use separate teaching methods for “chorus” students and “conductor” students, which complicates the integration between the two and affects the overall development of each group. To address this, teachers should create interactive scenarios where students can frequently switch roles, allowing each student to experience different perspectives. In summary, to enhance the overall level of chorus conductors in colleges and universities, teachers should innovate and improve the existing teaching methods, tailoring them to students’ needs to boost teaching efficiency.
There is no funding support for this study.