
This paper comprises the behavior of a non-stationary four-point SD technique that generates C\(^{4}\)-continuous limit curves using shape parameter \(\delta\)0. The asymptotically equivalence behavior and Laurent polynomial method is discussed to prove the convergence analysis and smoothness of the proposed technique.
Copyright © 2024 Iqra Abdul Razzaq, Mehran Azeem, Muhammad Ishaq, Murat Cancan and Mohammad Reza Farahani. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ubdivision surfaces were introduced in the late 1970’s in computer aided design. SD techniques are the essential tools that helps in the formation of smooth curves and surfaces. These help us to generate new shapes and curves with the help of the sets of control points that vary. It is an innovative technique that is used for the generation of the smooth surfaces as a sequence of successively refined polyhedral meshes. These SD techniques are currently extensively used in various fields such as computer graphics, solid modeling, computer game software, film animations and so on.
The idea to generalize a four-point SD technique to an interpolating SD technique came in 1990, described by Dyn, Gregory and Levin. An interpolating technique was at first defined over a triangular grid. A method is interpolating if the initial and all the subsequent generated control points remains in the mesh as the SD process proceeds. An approximating subdivision scheme was first introduced over a quadrilateral grid by Catmull and Clark in 1978. A process is called approximating if the limit curve includes only the newly generated control points. At each refining step the old control points get excluded. A SD technique is recursive in nature. The process of SD starts with initial polygon having discrete representation and then continues resulting in a smooth limiting curve. The existence of limit curves and their properties had to be introduced from the given finite number of coefficients, known as the generated mask of the SD technique, that defines the SD refinement rule. A repeated application of the SD rules generates the smooth surface, the process of refinement helps in how to add new vertices and averaging in where to add the new vertices. After the infinite number of refinements applied, a limit surface (or curve) is obtained. This curve is in much refined form as compared to the initial polygon. The analyzation of a non-stationary SD techniques includes a fixed refinement rules applied on a given set of points, but with the change in each refinement level, new points were introduced. The analysis of convergence is done by comparing the given technique with converging stationary SD technique, and similarly the analysis of smoothness is related to the derived first divided difference technique in stationary case. Similarly, by using the respective symbols and the z-transforms of given control points, it is possible to evaluate the convergence and smoothness of SD technique by simple algebraic operations.
SD techniques are iterative formulas for creation of smooth bends/ surfaces. These techniques lately turned into a fundamental piece of Computer aided designs. CAGD is basis tool that displays an art and respective data efficiently and expressively to the observer. It manages the scientific portrayal of shapes for use in Computer illustrations, numerical examination and estimate hypothesis. It is also helpful for processing image data received from the physical world.
P. Novara and L. Romani [1] exhibited 3 parameter joined ternary 4-to point subdivision conspire that gives a binding together system to a few autonomous propositions showed up in the writing. Z. Luo and W. Qi [2] utilized the technique for deducting interpolatory from approximating SD plot. S. Lin et al. [3] introduced another insertion subdivision plot for blended triangle/quad networks that is C1 continuous. C. Conti et al. [4] presented another proportionality idea among non-stationary SD plans named asymptotically likeness which is flimsier than asymptotically identicalness is presented and contemplated. J.Q Tan et al. [5] displayed another paired four-point SD plot which maintains the second control isolated contrast at the ancient apexes unaltered when the starting apexes are embedded. S.S Siddique et al. [6] displayed binary 3-point and 4-point non-stationary plans utilizing hyperbolic capacities as premise capacities. S.S. Siddique and M. Younis [7] built up a calculation to build m point (for any whole numbers) binary approaching SD plans utilizing Cox-de Boor recursion formula. S.S. Siddique and K. Rehan [8] improved a binary four-point resembling SD plot exhibited by Siddique and Ahmed (2006) by presenting worldwide tension parameter. G. Mustafa et al. [9] used the least quadrangles system for (2n)2-perceptions to fit berate cubic paranormal for \(n\geqslant 2\). G. Mustafa and R. Hameed [10] exhibited the groups of parameters subordinate univariate and bivariate SD plans. G. Mustafa and M. Bari [11] introduced varied extending groups of SD plans for suitable information to SD models. P. Novara and L. Romani [12] characterized the structure squares to acquire new groups of non-stationary SD plans. Bashir et al. [13] managed general methods of parameterized and non- parameterized bivariate SD plot with four parameters. M. Bari et al. [14] defined a method that is used to develope 3n-point quaternary approximating subdivision techniques. S.S. Siddique and T. Noreen [15] analyzed the property for six-point ternary interpolating subdivision technique that preserve convexity. H. Zheng and B. Zhang [16] presented a non-stationary combined subdivision technique that combines several approximating and interpolating subdivision techniques. P. Novara et al. [17] constructed a non-stationary subdivision scheme having several properties for 3 directional grids. M. Asghar et al. [18] introduced a simple way to increase the continuity of the subdivision schemes. G Kanwal et al. [19] developed a new numerical technique that defines a 6-point approximating subdivision techniques that helps in the generation of the smooth curves. S. A. Manan et al. [20] defines a technique to get the solution of 3rd order BV problem that is approximating 8-point scheme. G. Mustafa and S.T. Ejaz [21] introduced the two scale relation derivatives that are fulfilled by the subdivision technique and then used these results to construct the new subdivision method. G. Mustafa et al. [22] proposed a new iterative numerical approach that depends on interpolating subdivision techniques which gives the solution of four-point boundary value problems. G. Mustafa and R. Hameed [23] presented univariate and bivariate subdivision schemes forming families of parameter. J. Tan et al. [24] presented a non-stationary approximating 3-point SD scheme that helps in the generation of an vast variety of C3 continuous limit curves. L. Romani [25] presented a parameter-dependent RS subdivision algorithm. The newly generated C4 approximating subdivision technique has a wide range continuity that is broadly used in the field of geometric representations, movement and animations. For more details on C4 approximating subdivision technique, we refer the readers to [26–32].
A combined four-point SD technique generate C4 limiting curve. We are initially given the control set points \(s^{0} = \{{s_{i}^{0}\}}_{i \in z}\) at level 0, with the help of which we have to generate the new control points \(\{{s_{i}^{k + 1}\}}_{i \in z}\) at an optimized level k+1 using the SD technique. \[s_{2i}^{k + 1} = \left( \frac{1}{8} – \gamma \right)s_{i – 1}^{k} + \ \left( \frac{3}{4} + 2\gamma \right)s_{i}^{k} + \left( \frac{1}{8} – \gamma \right)s_{i + 1}^{k},\] \[\label{1}\tag{1} s_{2i + 1}^{k + 1} = \delta s_{i – 1}^{k} + \left( \frac{1}{2} – \delta \right)s_{i}^{k} + \left( \frac{1}{2} – \delta \right)s_{i + 1}^{k} + \delta s_{i + 2}^{k},\] where \(\gamma\) and \(\delta\) are the real constants.
Now, if we take \(\gamma\)= -2\(\delta\), we get the new control points as \[s_{2i}^{k + 1}= (\frac{1}{8} + 2\delta){\ s}_{i – 1}^{k} + (\frac{3}{4} – 4{\delta)\ s}_{i}^{k} + (\frac{1}{8} + 2{\delta)\ s}_{i + 1}^{k},\] \[\label{2}\tag{2} s_{2i + 1}^{k + 1}= \delta s_{i – 1}^{k} + \left( \frac{1}{2} – \ \delta \right)s_{i}^{k} + \left( \frac{1}{2} – \delta \right)s_{i + 1}^{k} + {\delta s}_{i + 2}^{k}\ ,\] which is also combined one and \(\gamma\) being the real constant.
Remark 1. This should be noted that for \(\gamma \neq – \frac{1}{16}\), the above given technique (1) reduces to an approximating SD. When \(\gamma\) =0, \(\frac{1}{32}\) the above given technique (1) is the cubic B-spline technique and quintic B-spline SD technique, correspondingly. If \(\gamma\) = \(\frac{1}{16}\), then the technique (1) would become interpolating SD technique. In particular, the above given technique (1) is the DD 4-point technique.
In respective section, we are going to deal with the Cl convergence of the above-mentioned combined technique (2). To get the Cl convergence of the combined SD technique (2), let us discuss the respective results:
Theorem 1. Let S is the stationary SD technique having symbol h(0)(z) and its respective jth order difference SD technique which is considered as \(S_j\) \((j= 1,..,n+1)\) exists with the following symbol h(j)(z) =\({(\frac{2z}{1 + z})}^{j}\) h(0)(z). Consider that the above-mentioned symbol satisfies
\[\sum\limits_{i}^{}h_{2i}^{(l)} = \sum\limits_{i}^{}h_{2i + 1}^{(l)} = 1, l= 0,1\ldots,n.\] If a relation L\(\geq\) 1 exists, such that \(\left\| {(\frac{1}{2}S_{n + 1})}^{L} \right\|_{\infty} < 1\), then the SD technique S will be Cn convergent, where \(\left\| {(\frac{1}{2}S_{n + 1})}^{K} \right\|_{\infty}\)= max\(\left\{ \sum\limits_{j}^{}{\left| g_{i – 2^{l}}^{|K|} \right|_{j}:0 \leq i \leq 2^{K}} \right\}\), g[K](z)= \(\prod\limits_{l = 0}^{K – 1}{g{(z}^{2^{l}}),}\) i(z) = \(\frac{1}{2}h^{(n + 1)}(z)\).
Following the statement of Theorem 1, we get the respective results on the Cl convergence of the SD technique mentioned in (2).
Corollary 1. The combined stationary SD technique (2) is
C0 convergent for \(\delta\ \in \ G_{0}\ : = \ \{\delta\ \in R^{2}:\ |\delta| + \left| \frac{3}{8} – 2\delta \right| + \left| \frac{1}{8} + \delta \right| < 1\}\),
C1 convergent for \(\delta\ \in \ G_{1}\ : = \ \{\delta\ \in R^{2}:\ 4|\delta| + \left| \frac{4}{8} – 4\delta \right| < 1,\ 4\left| \frac{1}{8} \right| < 1\}\),
C2 convergent for \(\delta\ \in \ G_{2}\ : = \ \{\delta\ \in R^{2}:\ 4|\delta| + 4\left| \frac{1}{8} – \delta \right| < 1\}\),
C3 convergent for \(\delta\ \in \ G_{3}\ : = \ \{\delta\ \in R^{2}:\ 16|\delta| < 1,\ 8\left| \frac{1}{8} – 2\delta \right| < 1\}\),
C4 convergent if \(\delta = \frac{1}{32}\).
Proof. The result that is obtained is a direct conclusion of Theorem 1 with taking in notice \(L=1.\) ◻
A non-stationary four-point SD technique is described by the refinement rules defined in section 2, since the respective control set points are defined as \[s_{2i}^{k + 1}= a_{0}^{k}s_{i – 1}^{k} + a_{1}^{k}{\ s}_{i}^{k} + a_{2}^{k}s_{i + 1}^{k},\] \[\label{3}\tag{3} s_{2i + 1}^{k + 1}= a_{3}^{k}s_{i – 2}^{k} + a_{4}^{k}s_{i – 1}^{k} + a_{5}^{k}\ s_{i}^{k} + a_{6}^{k}s_{i + 1}^{k},\] where \(s^{{^\circ}} = {\{ s_{i}^{0}\}}_{i \in Z}\) is the set of initial control points at very first level 0 and satisfies the relation \(a_{0}^{k} + a_{1}^{k} + a_{2}^{k} = 0\) and \(a_{3}^{k} + a_{4}^{k} + a_{5}^{k} + a_{6}^{k} = 0\) similarly.
The coefficients of a non-stationary SD technique are given by \[\begin{split} & a_{0}^{k}=\ \frac{1}{8} + 2s\left( \delta^{k + 1} \right) = a_{2}^{k}, a_{1}^{k}=\ \frac{3}{4} – 4s(\delta^{k + 1}),\\ & a_{3\ }^{k}=\ s(\delta^{k + 1})=a_{6}^{k}, a_{4}^{k}\ = \frac{1}{2} – s\left( \delta^{k + 1} \right) = a_{5}^{k}, \end{split}\] \[\label{4}\tag{4} s{(\delta}^{k + 1}) = \frac{1}{2\lbrack\left( \delta^{k + 1} \right)^{2} – 9\rbrack},\] with \[\label{5}\tag{5} \delta^{k + 1} = \sqrt{\delta^{k} + 20}, \beta^{0} \in \lbrack – 20, – 11) \cup ( – 11, + \infty).\] The coefficients {\(a_{i}^{k}\}\) thus be calculated at each arbitrary level k, where the initial parameter lies within domain \(\delta^0 \in [-20,-11) \cup (-11,\infty)\).
This must be noted that, starting from any \(\delta^0 \geq20\), we have \(\delta^0 +20 \geq 0, \forall k\in Z+\), so \(\delta^{k+1}\) is always well defined. Obtaining such a wide variety of definition enables us to achieve significant changes in structures of the limit curves.
Remark 2. From Eq. 5 and Figure 1 we can get that at first with small change in parameter \(\delta^{0}\) causes a change in the shape of the curve but as \(\delta^{0} \rightarrow \infty\), we get the approximation in the shape of the curve.
Remark 3. Following Eq. (5), if \(\ \delta^{0} = 5\), then\({\ \delta}^{k} = 5\),\(\forall\ k\ \in \ Z_{+}\), and above discussed sequence \(\left\{ \delta^{k} \right\}_{k \in N}\) is stationary. So the non-stationary SD technique converts to the respective stationary SD technique.
If\({\ \delta}^{0} > 5\), then\(\ \delta^{k} > 5\), above discussed sequence \(\left\{ \delta^{k} \right\}_{k \in N}\) decreases strictly, and \(\delta\) k converges to 5 as k\(\rightarrow \infty\).
If\(\ \delta^{0} < 5\), then\(\ \delta^{k} < 5\), above considered sequence \(\left\{ \delta^{k} \right\}_{k \in N}\) increases strictly, and \(\delta\) k again converges to 5 as \(k \rightarrow \infty.\)
Hence, from all above three cases we can deduce that for any given \(\delta^{0}\) in it’s defined, we have
\[\delta^{k} = 5\ \].
Here we do the convergence analysis of a non-stationary four-point SD technique Eq. 3 which generates C4 continuous limit curves for every value of the initial tension \(\delta^{0}\) in its respective domain provided in Eq. 5.
Theorem 2. A non-stationary technique defined by the coefficients in (4) is asymptotically equivalent to a stationary technique with coefficients in (2). Therefore, generates C4 continuous limit curves.
Proof. In order to prove that proposed non-stationary four-point technique is convergent to C4– continuous limit curve, we should evaluate its respective third divided difference mask. The mask of the technique is \[\begin{split} m^{k} = & \lbrack s(\delta^{k + 1}), \frac{1}{8} + 2 s(\delta^{k + 1}), \frac{1}{2} – s(\delta^{k + 1}), \\ & \frac{3}{4}- 4s(\delta^{k + 1}), \frac{1}{2}- s(\delta^{k + 1}), \frac{1}{8} + 2s(\delta^{k + 1}), \\ & s(\delta^{k + 1}) \rbrack. \end{split}\] Then, the corresponding first, second, third and fourth divided difference masks are given as
\[\begin{split} d_{(1)}^{k} =& 2 \left\lbrack s( \delta^{k + 1}) , \frac{1}{8} + s( \delta^{k + 1} ),\right. \\ & \frac{3}{8} – 2s( \delta^{k + 1} ), \frac{3}{8}- 2s( \delta^{k + 1} ), \frac{1}{8} + s( \delta^{k + 1} ),\\ & s( \delta^{k + 1} ) \Big\rbrack \\ d_{(2)}^{k}\ =& \ 4\ \left\lbrack\ s(\delta^{k + 1}),\ \frac{1}{8},\ \frac{2}{8}\ – 2\ s(\delta^{k + 1}),\ \frac{1}{8},\ s(\delta^{k + 1})\right\rbrack \\ d_{(3)}^{k}\ =& \ 8\ \left\lbrack\ s(\delta^{k + 1}),\ \frac{1}{8}\ – s(\delta^{k + 1}),\ \frac{1}{8}\ – s(\delta^{k + 1}),\right.\\ & s(\delta^{k + 1})\Big\rbrack \\ d_{(4)}^{k}\ =& \ 16\ \left\lbrack\ s(\delta^{k + 1}),\ \frac{1}{8}\ – 2\ s(\delta^{k + 1}),\ s(\delta^{k + 1})\right\rbrack. \end{split}\] Eq. 5 gives \[d_{(4)}^{k}\ = \ \lim_{k \rightarrow \infty}d_{(4)}^{k} = \ 16\left\lbrack\ \frac{1}{32},\ \frac{2}{32},\ \frac{1}{32}\right\rbrack.\] Which is exactly the mask of the fourth divided difference of the stationary technique. The stationary SD technique is C4 continuous, the technique that is going to associate with \(d^{\infty}_{(4)}\) will be C4.
The two technique are asymptotically equivalent, if \[\sum_{k = 0}^{+ \infty}{\| d_{(4)}^{k} – d_{(4)}^{\infty}\|} < + \infty.\] And we deduce that the technique assorted with \(d^{\infty}_{(4)}\) is C4, too. Since
\[\begin{aligned} d_{(4)}^{k}\ -d_{(4)}^{\infty}\ =& \ 16\left\lbrack s(\delta^{k + 1}) – \frac{1}{32},\ 2\ \left(\frac{1}{32} – s(\delta^{k + 1})\right),\right.\\ &\left.s(\delta^{k + 1})\ – \frac{1}{32}\right\rbrack \end{aligned}\]
\[{\| d_{(4)}^{k} – d_{(4)}^{\infty}\|}_{\infty} = 16\max\ \{ 2\ \left| s\left( \delta^{k + 1} \right) – \frac{1}{32} \right|,\] \[\ 2\left| \frac{1}{32} – s(\delta^{k + 1}) \right| = \ 32\left| s\left( \delta^{k + 1} \right) – \ \frac{1}{32} \right|.\]
To prove Eq. (5), we would prove the series convergence, that is defined as
\[\sum_{k = 0}^{+ \infty}\left| s\left( \delta^{k + 1} \right) – \frac{1}{32} \right|,\] which depend on the function \(s(\delta^{k + 1}\)). Now, as \(s(\delta^{k + 1})\) is expressed in the terms of the parameter \(\delta\)k+1through above discussed relation Eq. (4), we study the conduct of Eq. (5) as \(\delta\) k+1 varies from \([0, +\infty)\). As
\[\begin{split} s(\delta^{k + 1})\ – \ \frac{1}{32}\ &= \ 0\ \text{iff}\ \delta^{k + 1} = \ 5 ,\\ s(\delta^{k + 1}) – \ \frac{1}{32}\ &> 0\ \text{iff}\ \delta^{k + 1}\ \in \ (3,\ 5) ,\\ s(\delta^{k + 1})\ – \frac{1}{32} &< 0\ \text{iff}\ \delta^{k + 1}\ \in \ \lbrack 0,\ 3) \cup (5,\ + \infty). \end{split}\] Now we will discuss convergence of Eq. (5) relating following three distinct cases:
Case 1\(:\ \delta^{k + 1} = \ 5\ or\ \delta^{0}\ = \ 5\).
Since, we have \[\| d_{(4)}^{k} – d_{(4)}^{\infty}\|_{\infty} = 0.\] From this the convergence property of (5) follows.
Case 2: \(\delta^{k + 1}\ \in \ (3,5)\ or\ \delta^{0} \in \ ( – 11,5)\).
In this respective case,
\[\| d_{(4)}^{k} – d_{(4)}^{\infty}\|_{\infty} = 32\left\lbrack s(\delta^{k + 1}) – \frac{1}{32}\right\rbrack.\]
Hence, it is enough to prove
\[\begin{aligned} \sum_{k = 0}^{+ \infty} \left| s\left( \delta^{k + 1} \right) – \frac{1}{32} \right| &= \sum_{k = 0}^{+ \infty} \left( \frac{1}{2\left[ \left( \delta^{k + 1} \right)^{2} – 1 \right]} – \frac{1}{32} \right) \notag \\ & \qquad < + \infty. \end{aligned}\]
Now applying the ratio test. Since \(s(\delta^{k} + 1) – \frac{1}{32}\ > 0\) and the respective sequence\(\left\{ \delta^{k} \right\}_{k \in N}\) in this considered case is going to increase strictly, we have
\[\frac{\frac{1}{2\left\lbrack \left( \delta^{k + 2} \right)^{2} – 9 \right\rbrack} – \frac{1}{32}}{\frac{1}{2\left\lbrack \left( \beta^{k + 1} \right)^{2} – 9 \right\rbrack} – \frac{1}{32}} < 1.\]
So, the convergence property of Eq. (5) is proved.
Case 3: \(\delta^{k + 1}\ \in \ \lbrack 0,\ 3) \cup (5,\ \infty)\ or\ \delta^{0}\ \in \ \lbrack – 20,\ – 11)\ \cup \ (5,\infty)\).
In this observed case,
\[\| d_{(4)}^{k} – d_{(4)}^{\infty}\|_{\infty} = 32{[}\frac{1}{32} – s(\delta^{k + 1}){]}.\] Now, we prove \[\sum_{k = 0}^{+ \infty}\left| \frac{1}{32} – \ s\left( \delta^{k + 1} \right) \right|= \sum_{k = 0}^{+ \infty}{(\frac{1}{32} – \frac{1}{2\left\lbrack \left( \delta^{k + 1} \right)^{2} – 9 \right\rbrack}) < + \infty}.\] In the respective two subcases:
Case 3.1: \(\delta\)k+1 \(\in\) (5, \(\infty\)) or \(\delta\)o \(\in\) (5, \(\infty\)). Since the above-mentioned sequence \({\delta^k}_{k \epsilon N}\) in this case is going to decrease strictly, we have \[\frac{\frac{1}{2\lbrack{{(\delta}^{k + 2})}^{2} – 9\rbrack} – \frac{1}{\ 32}}{\frac{1}{2\lbrack\left( \delta^{k + 1} \right)^{2} – 9\rbrack} – \frac{1}{\ 32}} < 1.\] So, the convergence property of Eq. (5) is proved.
Case 3.2: \(\delta^{0} \in \lbrack – 20,\ – 11)\). We get \(\delta^{0} \in \lbrack 0,3)\) and \(\delta^{k}\) \(\in \ \)(3,5), ‘also true for higher values of k’ that expression converts to case 2. So, the convergence of Eq. (5) is confirmed.
Now considering the above discussed cases, we end up with the result that the non-stationary SD technique described by the coefficients in Eq. (3) is now asymptotically equivalent to the stationary defined in Eq. (2) and hence going to generate C3-continuous limit curves.
\[\frac{\frac{1}{2\lbrack{{(\delta}^{k + 2})}^{2} – 9\rbrack} – \frac{1}{32}}{\frac{1}{2\lbrack\left( \delta^{k + 1} \right)^{2} – 9\rbrack} – \frac{1}{32}} < 1.\] ◻
Basis function is defined as a limit function for initial data. The basis function of order one has the form:
\[n{[}x{]}= \left\{ \begin{matrix} 1\ &\text{if}\ 0 \leq x \leq 1 \\ 0\ &\text{otherwise}. \\ \end{matrix} \right.\ \ \]
This function is zero everywhere except where it is constant. i.e. [0,1)
Theorem 3. B, the basis function described by the proposed technique is symmetric along Y-axis.
Proof. Firstly, let consider a set \(D_p\) =\(\left\{ \frac{i}{2^{p}}|i\ \in Z \right\}\) such that B\((\frac{i}{2^{p}})\)=\(s_{i}^{p}\), \(\forall\) i\(\ \in\) Z. We prove this theorem with the help of induction principle applied on n.
For \(n=0,\)
\[B(i) = s_{i}^{o}=s_{- i}^{o} =B( – i).\] (by definition)
Thus, \[B\left(\frac{i}{2^{p}}\right) = B\left(\frac{- i}{2^{p}}\right) \forall\ i\ \in Z\ \text{for}\ \ p = 0.\]
Now, we let that the above relation is true for ‘k’ and we have to prove it for ‘k + 1’, \(\forall\ i \in Z\) \[\begin{split} B\left(\frac{2i}{2^{p + 1}}\right) &= a_{0}^{k}s_{i – 1}^{k} + a_{1}^{k}{\ s}_{i}^{k} + a_{2}^{k}s_{i + 1}^{k} ,\\ &= a_{0}^{k}B\left(\frac{i – 1}{2^{p}}\right) + a_{1}^{k}B\left(\frac{i}{2^{p}}\right) + a_{2}^{k}B\left(\frac{i + 1}{2^{p}}\right), \\ &= a_{0}^{k}B\left(\frac{- i + 1}{2^{p}}\right) + a_{1}^{k}B\left(\frac{- i}{2^{p}}\right)\\ &\qquad + a_{2}^{k}B\left(\frac{- i – 1}{2^{p}}\right), \\ &= B\left(- \frac{2i}{2^{p + 1}}\right),\ \forall\ i \in Z. \end{split}\] Similarly, we can prove \(B\left(\frac{2i + 1}{2^{p + 1}}\right)\)= \(B\left(- \frac{2i + 1}{2^{p + 1}}\right),\ \forall\ i \in Z\).
Hence, \(B\left(\frac{i}{2^{p}}\right) = B\left(\frac{- i}{2^{p}}\right)\), \(\forall\ i \in Z\). The proof of theorem is complete. ◻
In this respective section, we are now going to discuss the behavior of a proposed technique (5) considering an example. As discussed earlier in case (3.2) from inwards to outwards behavior of a discrete polygon as \(\delta^{0}\rightarrow \infty\).
In Figure (1), the geometric behavior of a non-stationary combined four-point subdivision technique is elaborated that generates C4 continuous limit curves for the wide range of C4 limiting curve using the formulated technique (5).
(a) \(g^0\) = -20, (b) \(g^0\) = -15, (c) \(g^0\) = -12, (d) \(g^0\) = -10, (e) \(g^0\) = -9, (f) \(g^0\) = -8, (g) \(g^0\) = -7,(h) \(g^0\) = -5, (i) \(g^0\) = -2, (j) \(g^0\) = 0 (k) \(g^0\) = 5, (l) \(g^0\) = 10, (m) \(g^0\) = 100, (n) \(g^0\) = 1000.
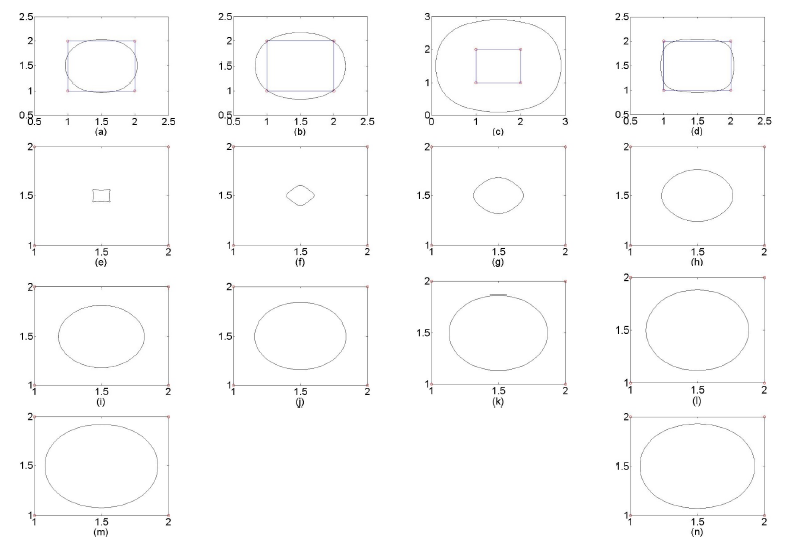
We presented a new non-stationary four-point SD technique which can generate C4 continuous limit curves. This new SD technique can generate limit curves for a very wide range (20,-11] \(\cup\) [-11, \(\infty\) ). The variation of parameters described the smoothness and flexibility of the proposed SD technique.