
The security of digital image transmission is related to the national economy and people’s livelihood, and the traditional text encryption algorithm performs poorly on images. Based on this, this paper designs the image encryption model, optimizes the generator and discriminator network structure based on the residual network model, and improves the generative adversarial network. Logistic chaotic system is utilized to construct a new GAN key generation model, and it is applied to the field of image encryption. On this basis, the Knuth-Durstenfeld algorithm is improved to complete the encryption of images from three processes: pixel value replacement, image disruption, and image diffusion, and applied research is carried out. The results show that the histograms of Lena and Peppers plaintext images show irregular statistical characteristics, and the gray value distribution pattern of the histograms of ciphertext images has no big ups and downs and tends to be stable and smooth. The correlation coefficients of adjacent pixels of ciphertext image are close to the ideal value of 0, and the image information is more difficult to be analyzed and deciphered. Under the noise attack, the PSNR values of the ciphertext image do not differ much, which can prove that the ability of anti-noise attack is good. The encryption algorithm based on generative adversarial network shows excellent performance on image encryption and protects the information security of digital images.
ith the rapid advancements in Internet and multimedia technologies, multimedia communication has emerged as a pivotal means for individuals to exchange information among themselves [1]. Concurrently, as people engage in the exchange of diverse information via the Internet, new requirements for information security in safeguarding confidential information during network transmission have arisen, gradually attracting research focus and attention [2,3].
Serving as a pivotal medium for information transmission, digital images occupy a significant role in facilitating the exchange of information. In the realm of network transmission and storage, numerous private and confidential images, encompassing patient medical records, as well as military and national defense-related sensitive imagery, are prevalent [4,5]. Should these images fall into unauthorized hands through illicit means, they pose a grave risk of exposing the user’s personal vital information, and in extreme cases, could potentially jeopardize national security. Consequently, the security of image information has garnered widespread attention among scholars [6,7].
Traditional image encryption algorithms commonly perceive digital images as sequences of binary data, subsequently encrypting these sequences using established data encryption methodologies, notably the Data Encryption Standard and the Advanced Encryption Standard [8]. Nevertheless, given the extensive information content inherent in digital images and the substantial redundancy among adjacent pixels, traditional encryption approaches necessitate substantial computational resources, with their security foundation resting on the intricacy of the underlying mathematical computations. In contrast, deep learning, a sophisticated machine learning paradigm, has garnered widespread application across diverse domains, encompassing target detection, image synthesis, speech recognition, and more. Notably, deep learning excels in its proficiency for intricate feature extraction and learning capabilities, enabling it to discern intricate patterns and characteristics within images [9,10].
In recent years, the realm of image encryption has witnessed the emergence of deep learning technology as a promising approach. The primary limitation of traditional image encryption algorithms stems from their reliance on a predefined set of equations, which contrasts with deep learning-based encryption methods. These latter algorithms, owing to their extensive computational models and intricate processes, exhibit an enhanced capability to withstand attacks, offering heightened encryption strength and improved security. Furthermore, they facilitate increased efficiency in image encryption, thereby accommodating a diverse array of scenarios and application demands [11].
In recent years, the rapid development of computer technology has led to a heightened concern among an increasing number of individuals regarding the issue of information security. Concurrently, the extensive utilization of digital images has necessitated the transmission of vast amounts of image information over networks, posing a risk of theft by unauthorized users during storage or transmission, ultimately resulting in information leakage. To address this challenge, image encryption emerges as a pivotal means for safeguarding the security of digital image information [12]. Jia, S. et al. have devised an encrypted image retrieval algorithm centered on scene understanding, which not only achieves a commendable level of retrieval accuracy but also enhances the security of users’ image privacy [13]. Additionally, Nguyen, T. S. et al. have proposed a cryptographic image reversal algorithm that utilizes the Absolute Moment Block Truncation Coding (AMBTC) algorithm as the fundamental architecture for reverse data hiding in encrypted images. In performance simulation tests, their algorithm has consistently outperformed traditional methods [14]. Tang, Z. et al. presented the significance of reversible data hiding (RDH) in safeguarding data information security and evaluated the efficacy of their proposed RDH algorithm when applied to encrypted images in a standardized benchmark image data test library, demonstrating exceptional embedding capacity [15]. Meanwhile, Ye, G. et al. formulated a novel multiple illusions image encryption method, incorporating compression-aware theory and Schur decomposition concepts, tailored to meet the stringent requirements of image privacy security in communication environments [16]. Furthermore, Li, X. et al. devised a hybrid mapping image encryption algorithm, integrating random arithmetic strategies from various randomized DNA encoding techniques, and conducted thorough experiments which revealed the algorithm’s capacity to withstand typical information attacks [17].
In the realm of multimedia information, image information has emerged as a pivotal means of human expression due to its vivid depiction. However, it encompasses classified image data, such as military equipment deployment diagrams and confidential drawings pertaining to industries like business and construction, which necessitate encryption prior to transmission over networks. Hu, G. F. refined the concept of quantum image flexible representation and devised an advanced quantum image encryption algorithm, thereby bolstering the privacy and security of image transmission [18]. Abd-Alhameed, R. A. introduced a capacitive hyperchaotic system grounded in four-dimensional fractional order memory theory, incorporating an encryption system for image transmission within the framework to ensure efficient and stable realization of image encryption protection [19]. Farwa, S. et al. examined the viability of a scheme that integrates the algebraic substitution box effect and the Arnold transform dislocation effect for image encryption. Through experimental and statistical analysis, they demonstrated the scheme’s ability to achieve image encryption and safeguard against cyber-attacks [20]. Kumar, P. et al. pioneered an algorithm for the fusion generation of medical and visual images, leveraging the principle of non-downsampled shearlet transform for structural composition. The images generated by this algorithm exhibited superior definition, precision, and other desirable qualities in functional testing [21].
In this paper, we first propose a generative adversarial network (GAN) framework grounded on the residual network model. Subsequently, we optimize both the generator network and the discriminator network structures individually to enhance the stability of the training process. Furthermore, we incorporate the Wasserstein distance to address the limitations of the loss function. Subsequently, we construct a novel GAN-based key generation model tailored to the requirements of image encryption security, leveraging the Logistic chaotic system.To this end, we develop the overall architecture of an image encryption algorithm by refining the Knuth-Durstenfeld algorithm. This encryption approach encompasses three primary facets: pixel value substitution, image disruption, and image diffusion. Ultimately, we conduct experimental evaluations of the devised encryption system, subjecting the ciphertext images to a rigorous analysis encompassing histogram analysis, neighboring pixel correlation assessment, robustness testing, and resistance analysis against differential attacks. These analyses aim to comprehensively evaluate and demonstrate the encryption performance of the proposed algorithm on image data.
The basic structure of ResNet is similar to the convolutional neural network, the difference is that ResNet adds a special residual module, and the basic structure of the residual module is shown in Figure 1.
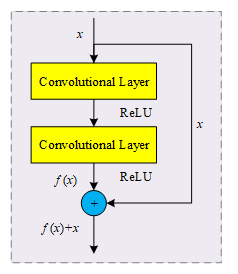
Residual module Figure 1 shows that \(x\) skips two convolutional layers from the right, this structure is called “jump connection”, the residual module is constructed with this connection as the core. Assuming that the mapping of the two convolutional layers in Figure 1 is \(f\left(x\right)\), if the “jump connection” on the right is not added, the input \(x\) will be mapped by \(f\left(x\right)\) to get \(H\left(x\right)\), and the output of the network is shown in (1). \[\label{GrindEQ__1_} H\left(x\right)=f\left(x\right). \tag{1}\] After adding “jump connection”, the output is shown in (2). \[\label{GrindEQ__2_} H\left(x\right)=f\left(x\right)+x . \tag{2}\] In the deep network, it is easy to appear the phenomenon of decreasing effect, at this time, the input can be made equal to the output, skipping the mapping process of decreasing effect, i.e., \(H\left(x\right)=x\). For the ordinary convolutional network, whose output is \(H\left(x\right)=f\left(x\right)\), in order to make \(H\left(x\right)=x\), it is necessary to train the neural network to make \(f\left(x\right)=x\), which is difficult to realize: however, for the residual network, it only needs to be \(f\left(x\right)=0\), which can be converted into \(H\left(x\right)=f\left(x\right)+x\) to \(H\left(x\right)=x\), and the operation is relatively simple to eliminate the undesirable effect of the network layer mapping that is equivalent to directly cropping the convolutional layer.
In this paper, an improved one-dimensional residual generative adversarial network is proposed based on the GAN model. Firstly, the problem of network degradation is improved by introducing the residual module to improve the training stability; then, the neural network in the GAN is replaced by a one-dimensional convolutional network to make the network more compatible with the generation of one-dimensional sequences: finally, a suitable loss function is chosen to make the training more efficient and stable. The \(G\) network structure of the model is shown in Figure 2.

The structure of the discriminator network (\(D\) network) of 1D-RGAN is shown in Fig. 3. First, the convolutional layer is responsible for feature extraction, which uses the LeakyReLU activation function. Second, the Flatten layer compresses the data into one-dimensional data between the convolutional layer and the fully connected layer. Then, the Dropout layer is more effective in mitigating the occurrence of overfitting: finally, the output layer uses the tanh activation function instead of the original GAN’s sigmoid activation function due to the choice of the loss function in the later section, which makes the output of the \(D\)-network no longer a binary classification problem between 0 and 1.

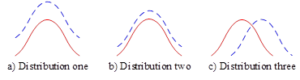
The JS scatter is illustrated schematically in Figure 4. Specifically, the dashed and solid lines depict two distinct distributions. Notably, the distance separating these distributions in Figure 4(b) is visibly closer than that in Figure 4(a). However, owing to the absence of intersection between them, this results in a constant scatter and a gradient of zero. Consequently, the loss function fails to be positively influenced by alterations in the network parameters, rendering the optimization of the network challenging. It is only when these two distributions intersect, as exemplified in Figure 4(c), that the loss function acquires significance, enabling the proper optimization of network parameters.
In this paper, Wasserstein distance (\(W\) distance) is introduced as a loss function to solve this problem. The value of \(W\) distance measures the distance between two distributions, as shown in (3). First, the set of all paths from \(P_{2}\) training to \(P_{t}\) is obtained by calculation: then, the distance of the shortest path between \(P_{t}\) and \(P_{2}\), i.e., W distance, is obtained from it. Even if the two distributions do not overlap, the W distance still reflects the distance of their distributions. \[\label{GrindEQ__3_} W_{\left[P_{t} ,P_{p} \right]} ={\mathop{\inf }\limits_{\gamma \in \Pi \left[P_{t} ,P_{p} \right]}} {\int\!\!\!\!\int}\gamma \left(x,y\right)d\left(x,y\right)dxdy , \tag{3}\] where \(\prod \left[P_{r} ,P_{R} \right]\) is joint distribution of \(P_{r}\) and \(P_{g}\), \(P_{r}\) is true distribution, \(P_{g}\) is generative distribution and \(Inf\) is lower bound for the function value.
However, there exists a restriction on the use of the \(W\) distance as a loss function for the \(D\) network, namely the Lipschitz continuum. Its adds a restriction to the continuous function \(f\) by requiring the existence of a constant \(K\ge 0\) such that any two elements \(x_{1}\) and \(x_{2}\) in the domain of definition satisfy (4). In layman’s terms, the Lipschitz restriction is the requirement that the function \(f\) is foot-stoppingly affine in the domain of definition. In order to satisfy this condition, the authors of WGAN restrict all the parameters of the neural network \(w\), to the range \(\left[-c,c\right]\), when there must exist some constant \(K\) such that the local variation of the function does not exceed the restriction. \[\label{GrindEQ__4_} \left|f\left(x_{1} \right)-f\left(x_{2} \right)\right|\le K\left|x_{1} -x_{2} \right| . \tag{4}\] However, limiting the parameter range to \(\left[-c,c\right]\) may cause problems such as vanishing gradients and gradient explosion. Only if \(c\) is set appropriately, the network can be trained properly. However, it is difficult for that tuning parameter to work smoothly in practical applications. So in this paper, the gradient penalty mechanism proposed by WGAN-GP is used to solve the problem. The gradient penalty satisfies the Lipschitz continuous constraints by setting an additional loss term, and the loss function of the D network in this paper is shown in (5). \[\label{GrindEQ__5_} \begin{array}{rcl} {L\left(D\right)} & {=} & {-E_{x-p_{f} } \left[D\left(x\right)\right]+E_{x-p_{f} } \left[D\left(x\right)\right]} \\ {} & {} & {+\lambda E_{x-p_{1} } \left[\left\| \nabla _{x} D\left(x\right)\right\| _{p} -1\right]^{2} }, \end{array} \tag{5}\] where \(\nabla\) is the sign of the gradient and \(P_{x}\) is the distribution of random sampling points on the line connecting the real and generated data.
The gradient penalization method involves the process of mixing the true and generated samples. First, a pair of true and false samples \(x_{r} \in P_{r}\), \(x_{2} \in P_{2}\) are randomly sampled, then a random number \(\alpha =uniform\left[0,1\right]\) is taken and finally sampled on the line connecting \(x_{r}\) and \(x_{2}\), the sampling method is shown in (6). The mixing data consists of the set of \(\hat{x}\), whose distribution is \(P_{x}\). The mixing data is fed into the mixing output (mix_output) obtained from the \(D\) network, which will be involved in the computation of the loss values of the \(D\) network and the \(G\) network. \[\label{GrindEQ__6_} \hat{x}=\alpha x_{r} +\left(1-\alpha \right)x_{2} . \tag{6}\]
The GP term in Eq. (5) is shown in Eq. (7). By adding the GP term and calculating the gradient of the three loss values, the gradient of the 1 network can effectively meet the requirement that the gradient of the \(D\) network does not exceed \(K\) so that the loss function is smooth within a certain range. In summary, in this paper, the \(W\) distance with GP term will be used as the loss function of the 1-dimensional convolutional generative adversarial network. \[\label{GrindEQ__7_} \lambda E_{x\sim P_{3} } \left[\left\| \nabla _{x} D\left(x\right)\right\| _{p} -1\right]^{2} . \tag{7}\]
In this section, an improved chaotic system is proposed for the problem of insufficient randomness of Logistic chaotic system, a new GAN key generation model is constructed, and finally, the performance and randomness of pseudo-random sequences generated by the GAN key generation model are verified, which proves that it can be applied to the field of image encryption.
Based on Logistic chaotic system, an improved quadratic chaotic system is proposed as shown in (8). \[\label{GrindEQ__8_} x_{t+1} =\text{mod}\left(a+\left(1-8x_{t} \right)^{2} ,1\right),\left(0<x_{t} <1,i=1,2,\ldots \right) , \tag{8}\] where \(mod\) is mode-taking operation and \(a\) is control parameters.
This chaotic system parameter \(a\ge 0\), the range of parameters is increased than the Logistic chaotic system parameter range, the chaotic sequence generated by iteration is more uniformly distributed in the whole space. In order to make the chaotic system dynamics behavior more complex, the chaos interval is larger, the control parameters of the system are more, and more to meet the security needs of image encryption, this paper proposes an improved cubic chaotic system based on the Logistic chaotic system, the formula is shown in (9). \[\label{GrindEQ__9_} x_{t+1} =\sin \left(a-bx_{t} \left(1-8x_{i} \right)^{2} \right),\left(0<x_{t} <1,i=1,2,\ldots \right), \tag{9}\] where control parameter \(a\ge 0\), control parameter \(b\in \left(-\infty ,+\infty \right)\), the system has more control parameters and a wider range of chaos.
In this paper, we design a new key flow generation model called GAN key generation model using the 1D-RGAN and chaotic system designed above, and the structure is shown in Figure 5.
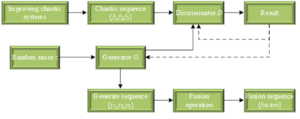
The steps of training model and key generation are as follows:
Step 1: Generate three chaotic sequences \(f_{1}\), \(f_{2}\) and \(f_{3}\) as real data under different initial conditions using the new chaotic system.
Step 2: Input the real data to the discriminator: generate a normally distributed random noise between \(\left[0,1\right]\) to input to the generator. The generator and the discriminator are trained according to the algorithm and after the training, the generator generates random sequences \(y_{1}\), \(y_{2}\) and \(y_{3}\).
Step 3: Fuse \(y_{1}\), \(y_{2}\) and \(y_{3}\) to generate the fused random sequence \(fusion\left(i\right)i=1,2,\ldots ,M\times N\). \(fusion\left(i\right)\) is computed as follows, first quantize the values of the three sequences into the interval [0, 255] to obtain the decimal quantized sequences \(s_{1}\), \(s_{2}\) and \(s_{3}\). \[\label{GrindEQ__10_} s_{1} (i)=\text{mod}\left(y_{1} (i)y_{2} (i)-y_{3} (i),256\right), \tag{10}\] \[\label{GrindEQ__11_} s_{2} \left(i\right)=\text{mod}\left(y_{1} \left(i\right)+s_{1}^{2} \left(i\right),256\right), \tag{11}\] \[\label{GrindEQ__12_} s_{3} \left(i\right)=\text{mod}\left(y_{2} \left(i\right)+s_{2}^{2} \left(i\right),256\right). \tag{12}\] Then, in order to sufficiently disrupt the correlation between the sequences, the intermediate sequences \(middle\), \(m_{1}\) and \(m_{2}\) are computed. when \(i=1\), the first value of the sequence is computed. \[\label{GrindEQ__13_} \text{middle}\left(1\right)=\text{mod}\left(s_{1} \left(1\right)s_{2} \left(1\right)-s_{3} \left(1\right),256\right), \tag{13}\] \[\label{GrindEQ__14_} m_{1} \left(1\right)=\text{mod}\left(\text{middle}\left(1\right)^{2} +s_{1} \left(1\right),256\right), \tag{14}\] \[\label{GrindEQ__15_} m_{2} \left(1\right)=\text{mod}\left(\left(m_{1} \left(1\right)\right)^{2} +s_{2} \left(1\right),256\right). \tag{15}\] When \(1<i\le M\times N\), the intermediate sequences \(middle\left(i\right)\), \(m_{1} \left(i\right)\), and \(m_{2} \left(i\right)\) are computed, correlating the value in bit \(i\) with the value in bit \(i-1\). \[\label{GrindEQ__16_} \text{middle}\left(i\right)=\text{mod}\left(s_{1} \left(i\right)s_{2} \left(i\right)-\text{middle}\left(i-1\right),256\right), \tag{16}\] \[\label{GrindEQ__17_} m_{1} \left(i\right)=\text{mod}\left(\text{middle}\left(i\right)^{2} +s_{1} \left(i\right),256\right), \tag{17}\] \[\label{GrindEQ__18_} m_{2} \left(i\right)=\text{mod}\left(m_{1} \left(i\right)^{2} +s_{2} \left(i\right),256\right). \tag{18}\] Finally, the fusion sequence \(\text{fusion}\left(i\right)\) is calculated as shown in (19). \[\label{GrindEQ__19_} \text{fusion}\left(i\right)=\text{mod}\left(m_{1} \left(i\right)+m_{2} \left(i\right),256\right)i=1,2,\ldots ,M\times N . \tag{19}\]
Step 4: Save the model parameters so that the generator for the GAN key generation model can be invoked directly.
The Knuth-Durstenfeld algorithm stands as one of the seminal shuffling algorithms, whose concept is rooted in card drawing, swapping, and insertion mechanisms. Specifically, the Fisher-Yates Shuffle algorithm aligns with the card drawing paradigm, aiming to randomly extract data from the original data set without repetition, thereby introducing a certain level of randomness. Conversely, the Knuth-Durstenfeld algorithm, akin to card swapping, refines the Fisher-Yates approach by initiating the traversal from the tail of the array. In this method, an unprocessed element is randomly exchanged with the current tail element of the array, whereupon the tail advances, and the process repeats until all elements have been traversed. Notably, this algorithm eschews the use of an auxiliary array for data storage, contributing to its reduced space and time complexity.
However, the direct application of the Knuth-Durstenfeld shuffling algorithm in image encryption encounters limitations. The primary obstacles are twofold: firstly, the original algorithm’s random number generator is incapable of reproducing the exact sequence during decryption, thus hindering successful decryption, as it fails to mirror the encryption process’s randomness. Secondly, as the algorithm progresses, the unprocessed data in the array diminishes, leading to a corresponding decrease in the random number generator’s range. Notably, both chaotic sequences are confined to a fixed range and do not diminish with iteration. To address these issues, this paper proposes an enhancement to the Knuth-Durstenfeld algorithm by substituting the random number generator with a sequence generated by a chaotic system. Furthermore, the implementation incorporates a modulo function to ensure that the generated random numbers remain within the bounds of the unprocessed data array, thereby overcoming the aforementioned limitations.
The overall flowchart of the proposed Generative Adversarial Network (GAN)-based image encryption algorithm incorporating plaintext correlation is presented in Figure 6. This algorithm is systematically divided into two distinct phases. The initial phase pertains to key generation, where the key generation network undergoes training to establish a mapping from the original image to a key style image. Notably, the key style image is chosen as a highly random, uniformly distributed image, enabling the network to generate a corresponding key image tailored to the input original image. This generated key is inherently linked to the plaintext, thereby enhancing the security level of the associated encryption algorithm. Within the framework of this paper’s encryption algorithm, the initial step involves inputting the original image into the key generator to retrieve the corresponding key.The subsequent phase constitutes the encryption stage, where the generated key image is transformed into a matrix representation of a random sequence. Subsequently, the encryption of the original image is accomplished through a series of operations: pixel value substitution, image disambiguation, and image diffusion, ultimately yielding the ciphertext image. The decryption process is simply the reverse of the encryption procedure, underscoring the symmetric nature of the overall encryption algorithm. Consequently, the decrypted image remains identical to the original image, ensuring data integrity throughout the encryption-decryption cycle.
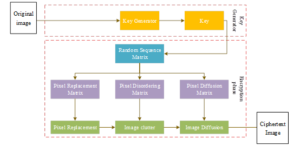
The encryption algorithm presented in this paper leverages the key image, generated from the input original image during the key generation stage, and subsequently transformed into a matrix of random numbers. This matrix then facilitates the encryption of the image through a comprehensive process comprising three distinct steps: pixel value substitution, image disambiguation, and image diffusion. This orchestrated sequence of operations culminates in the production of a high-security ciphertext image.
The first stage of the encryption scheme is the pixel value replacement, corresponding to the key image generated by the key generation network, which is converted into three pixel value replacement matrices based on the RGB three-channel information of the key image \(PR_{mat{\rm \; }}\). Through the pixel value replacement formula, the operation is performed on the three channels corresponding to the plaintext image, and a new pixel value is obtained to replace the original pixel value of the plaintext image, which completes the first encryption step and obtains the replacement image. The pixel replacement formula is shown in (20). \[\label{GrindEQ__20_} \text{NewValue}=\left(\text{ImageList}\left[\text{index}\right]+\text{KeyList}\left[\text{index}\right]\right)\% \left(256\right), \tag{20}\] where ImageList is the pixel matrix of the original image, index is the corresponding coordinate value, KeyList is the pixel replacement matrix to which the key image is converted, and New Value is the new pixel value at the current position after replacement. Figure 7 demonstrates how the pixel value replacement process operates on a 4\(\mathrm{\times}\)4 pixel matrix.

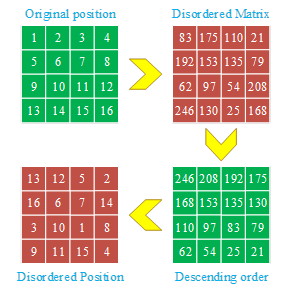
The key image generated by the key generation network is converted into three disordered matrices \(PR_{mat}\) in the image disarray stage, indexed with the replacement image after pixel value replacement is completed in the previous stage, and the position information in the replacement image corresponds one-to-one with the position in the disordered matrices, and the values of the three disordered matrices \(PR_{mat}\) are rearranged in accordance with the ascending or descending algorithm in the image disarray stage, and the corresponding replacement image follows the rearranged matrix to disrupt the original position, and the replacement image completes the image disarray process with the ordering of the disordered matrix, obtaining the disarrayed image. The corresponding replacement images will follow the rearrangement of the disordered matrices to disrupt the original positions, and the replacement images are sorted with the disordered matrices to complete the image disruption process and obtain the disrupted image. In Fig. 8, it is demonstrated how the image disarrangement algorithm can be accomplished by using the descending order within a 4\(\mathrm{\times}\)4 pixel matrix.
In the algorithm of this chapter, the scrambled image obtained after the image scrambling stage is converted into binary form by converting the pixel values in each plane of the RGB channel, and the pixel values of the three random number matrices \(PR_{mat}\) of the key image are also converted into binary form, which are then used in the different-or-ortho (XOR) operation with the binary pixel values of each corresponding position in the scrambled image to get the new pixel values, which are then assigned to the corresponding positions and the three matrices after the operation are recombined into a three-channel image to get the final ciphertext image. The three matrices after the operation are recombined into a three-channel image, and the final ciphertext image is obtained. The encryption algorithm designed in this chapter realizes the diffusion phase of the encrypted image through the different-or operation, which enhances the security of the ciphertext image.
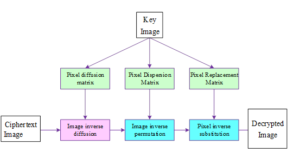
The encryption algorithm introduced in this paper adheres to a symmetric encryption paradigm, where the decryption process serves as the inverse mirror of its encryption counterpart, necessitating possession of the encryption key by the decrypting party. During encryption, the algorithm sequentially executes three primary operations: pixel value substitution, followed by disorganization of the substituted results, and concluding with diffusion on the disorganized matrix. Consequently, the decryption process reverses this order, as illustrated in Figure 9. Initially, an inverse diffusion operation is applied to the ciphertext image, subsequently, the disrupted order is reinstated using the same sorting algorithm employed during disorganization, and finally, an inverse pixel value replacement is executed to yield the decrypted image. Given the reversibility of the proposed encryption scheme, the decrypted image remains identical to the original plaintext image.
In this experimental setup, we employed standard grayscale images of Lena, Peppers, Baboon, and Airplane, each with dimensions of 512\(\mathrm{\times}\)512 pixels, as our test subjects. The outcomes of the encryption and subsequent decryption processes applied to these images are presented in Figure 10. Upon inspection, it becomes evident that the visual fidelity between the original plaintext image and its decrypted counterpart is impeccable, demonstrating a perfect match. Furthermore, the encrypted images resemble a chaotic noise pattern, devoid of any discernible or effective information leakage, thereby validating the security of the encryption method.
Histogram serves as a prevalent criterion for assessing the experimental outcomes of image encryption algorithms. For an encryption algorithm to demonstrate superior performance, the histogram of its resulting ciphertext image ought to exhibit uniformity. In this study, the images of Lena and Peppers have been chosen as the experimental subjects for investigation.
The analysis of the histograms for the plaintext and ciphertext of Lena and Peppers images is presented in Figure 10. Inspection of the figure reveals that the histograms of the plaintext images exhibit irregular statistical distributions. Specifically, Lena’s plaintext image displays a peak in statistical frequency within the gray value interval of 15-25, while Peppers’ plaintext image exhibits a similar peak within the range of 65-70. In contrast, the histogram of the ciphertext image reveals a stable and flat gray value distribution, devoid of significant fluctuations. These experimental outcomes demonstrate that the proposed algorithm effectively obscures the statistical properties of the gray values in the test images, thereby exhibiting robust diffusion characteristics and resilience against statistical attacks.

The original image exhibits a considerable degree of correlation among neighboring pixels. When this correlation is pronounced, an attacker may readily extract image information through statistical analysis. Conversely, as the correlation coefficient between pixels approaches zero, statistical analysis attacks become increasingly challenging, thereby enhancing the security of the encryption algorithm.
The outcomes of the correlation analysis experiment are detailed in Table 1, which compares the correlation coefficients of grayscale images against a benchmark. A correlation coefficient value approaching 1 signifies a strong correlation among pixels, whereas values nearing 0 indicate a weaker correlation. Notably, the experimental ciphertext images of Lena and Peppers exhibit correlation coefficients highly proximal to the ideal value of 0, in contrast to the plaintext images, whose correlation coefficients tend towards 1. This observation attests to the effective scrambling of the experimental ciphertext images, where pixels have been thoroughly rearranged and dispersed, rendering the image information more resilient to analysis and decryption. Consequently, the experimental results validate that the proposed scheme significantly reduces the correlation among image pixels, thereby demonstrating a commendable encryption efficacy.
| Lena | Peppers | All black | All white | ||
| Plaintext image | Horizontal direction | 0.9465 | 0.9814 | NaN | NaN |
| Vertical direction | 0.9610 | 0.9598 | NaN | NaN | |
| Diagonal direction | 0.9016 | 0.9238 | NaN | NaN | |
| Ciphertext image | Horizontal direction | -0.0051 | 0.0053 | -0.0072 | -0.0068 |
| Vertical direction | -0.0058 | 0.0051 | -0.0134 | -0.0023 | |
| Diagonal direction | -0.0014 | 0.0018 | 0.0042 | -0.0018 |
In order to verify the robustness of the algorithms in this chapter, this chapter analyzes the proposed algorithms from two aspects: noise attack and cropping attack.
The robustness of the proposed algorithm is analyzed from two aspects.
Embedding the ciphertext within a carrier image offers visual obscurity during transmission and the associated encryption key serves as a deterrent against attacks. Nevertheless, the visually secure image may be subjected to various assaults during transmission, including noise contamination and data loss, which can complicate the process of image decryption. Consequently, a thorough analysis of the algorithm’s resilience against such attacks is imperative.
The peak signal-to-noise ratio (PSNR) values under noise attack are shown in Table 2. It can be seen that whether it is Gaussian noise or Pepper noise, the PSNR value decreases with the increase in the degree of added noise. When the degree of noise is 0.0002, the PSNR value is the largest, which is 36.1592 under Gaussian noise and 36.5694 under pretzel noise. moreover, the PSNR values of the four images do not differ much under various degrees of noise attacks, which indicates that each image is affected by the noise attack in a more average way, and each steganographic image is affected by the basically the same.
| Attack | Gaussian noise | Salt-and-pepper noise | |||||||
| Variance/noise density | 0.0002 | 0.0004 | 0.0006 | 0.0008 | 0.0002 | 0.0004 | 0.0006 | 0.0008 | |
| This algorithm | Lena | 36.1592 | 35.9876 | 35.1258 | 35.0921 | 36.5694 | 35.8714 | 35.2164 | 34.4164 |
| Peppers | 37.2413 | 36.5496 | 36.3984 | 36.1891 | 37.0130 | 37.4851 | 36.1456 | 35.9741 | |
| Baboon | 34.4896 | 34.2897 | 34.1651 | 34.0236 | 34.3684 | 33.8974 | 33.0478 | 32.1026 | |
| Airplane | 34.0124 | 33.9874 | 33.6875 | 33.1052 | 35.2189 | 35.0127 | 34.6587 | 34.3697 | |
To test the robustness of cropping attack, the ciphertext image is cropped in different sizes and decrypted in the same steps. The Lena image is used as the test image. To further evaluate the quality of decrypted image after cropping attack, the values of PSNR and SSIM of plaintext image and recovered image can be calculated to measure and evaluate the difference between different decrypted images.
The values of SSIM and PSNR against cropping and pepper noise are shown in Table 3. From the table, it can be seen that all the values of PSNR are greater than 40dB and all the values of SSIM are close to 1, which proves that the proposed algorithm can effectively resist noise and cropping attacks.
| Attack mode | Evaluation index | Lena | Peppers | Baboon | Airplane |
| Data loss | PSNR | 46.1254 | 45.8654 | 44.9743 | 47.8745 |
| (64\(\mathrm{\times}\)64) | SSIM | 0.7941 | 0.8436 | 0.9784 | 0.7746 |
| Noise attack | PSNR | 47.6845 | 46.4789 | 45.9648 | 43.9876 |
| (0.01) | SSIM | 0.8761 | 0.8974 | 0.9741 | 0.8111 |
Optimal encryption algorithms ought to exhibit robust resistance against differential attacks, characterized by a marked disparity in encryption efficacy when subtle alterations are introduced to the plaintext image utilized for encryption. This feature hinders attackers from extracting meaningful information from the encrypted image. Two key metrics commonly employed to assess an algorithm’s resilience against differential attacks are the Number of Pixels Change Rate (NPCR) and the Uniform Average Change Intensity (UACI). Specifically, NPCR quantifies the percentage of pixel alterations in the corresponding ciphertext image resulting from a random change in a single pixel’s value within the plaintext image. Meanwhile, UACI measures the intensity variation in the pixel values of the corresponding ciphertext image when a single pixel’s value undergoes a change.
The results of the simulation experiments pertaining to the Number of Pixels Change Rate (NPCR) and Uniform Average Change Intensity (UACI) are presented in Table 4, alongside a comparative analysis. As evident from the table, the NPCR simulation outcomes achieved by the algorithm proposed in this paper approximate the ideal value of 1, surpassing those of other algorithms. This indicates a superior competitive edge, thereby attesting to the algorithm’s robust performance against differential attacks and its high security prowess.
| Encrypted image | Textual algorithm | 3D image encryption algorithm | PSO-BP neural network algorithm | DNA cross mutation encryption algorithm | Piecewise chaotic mapping algorithm | |
| NPCR | Lena | 0.9986. | 0.9978 | 0.9912 | 1.0461 | 0.9949 |
| Peppers | 0.9967 | 0.9605 | 0.9935 | 0.9953 | 0.9925 | |
| Camera | 0.9961 | 0.9871 | 0.9967 | 0.9345 | 0.9934 | |
| UACI | Lena | 0.4398 | 0.4056 | 0.3974 | 0.4196 | 0.4311 |
| Peppers | 0.4257 | 0.4185 | 0.4186 | 0.4177 | 0.4209 | |
| Camera | 0.4305 | 0.4113 | 0.4165 | 0.4231 | 0.4298 |
GAN generates a model of chaotic sequences that can be used to reconstruct the chaotic sequence of the generated chaos, but the attacker must know that GAN is competing against the parameters, the initial state of the generated network and the arrangement of the matrix. At the same time, the attacker can use the method of poor attack to guess the key, but this method will produce high cost in calculation. Of course, the attacker can also use other methods such as plain attack, difference attack and linear attack method to attack the model, and if you use these three methods, you must solve the network’s parameters, the initial values and the input, which is extremely difficult in the case of the secret text.
This paper presents a novel image encryption algorithm, integrating the GAN-based key generation model with the Knuth-Durstenfeld shuffling algorithm. The subsequent conclusions are drawn based on a comprehensive analysis of the following aspects: the histogram distribution of the ciphertext image, the correlation among neighboring pixels, the algorithm’s robustness, and its resistance to differential attacks.
The histogram of the plaintext image exhibits irregular statistical characteristics, with Lena’s plaintext image displaying the highest frequency of gray values within the range of 15-25, whereas Peppers’ plaintext image exhibits the peak frequency in the range of 65-70. Conversely, the gray value distribution of the ciphertext image’s histogram remains relatively stable and smooth, devoid of significant fluctuations.
The correlation coefficients of the experimental ciphertext images, Lena and Peppers, closely approximate the ideal value of 0, whereas the correlation coefficients of the corresponding plaintext images tend towards 1. This validates that the experimental ciphertext images undergo effective scrambling, with their pixels being thoroughly rearranged and dispersed. Consequently, the information contained within these images becomes more challenging to analyze and decrypt. This underscores the algorithm’s efficacy in diminishing pixel correlation and demonstrates its impressive encryption performance.
The SSIM (Structural Similarity Index Measure) and PSNR (Peak Signal-to-Noise Ratio) values, evaluated against cropping and pepper noise attacks, consistently exceed 40dB, with SSIM values nearing unity. This robust performance substantiates the algorithm’s capability to effectively withstand noise and cropping attacks, highlighting its resilience and suitability for secure image transmission and storage.
The simulation experimental results of the Number of Pixels Change Rate (NPCR) obtained using the algorithm presented in this paper are proximal to the ideal value of 1, consistently surpassing those achieved by other algorithms. This competitive edge underscores the algorithm’s exceptional performance in resisting differential attacks, thereby contributing to its heightened security capabilities.
Although the model of the paper has been preliminarily implemented, in the future research, there is a lot of experiments, the evaluation of the sorting parameters, and the ability to continue to improve the performance of the encryption method.
This work was supported by the Science and Technology Project of Henan (Optical image compression and encryption based on depth learning and high-quality reconstruction, 242102210058).