
Analyzing and predicting the behavior of students in colleges and universities is very important for the growth and development of students and for teachers to test their teaching results. In this paper, after using DT-kmeans clustering algorithm to analyze the density of students’ behavioral features, the center point of the class clusters is selected and it is iteratively updated to realize the cluster analysis of students’ behavior. Then the entropy weight method is used to calculate the weight of each behavioral feature to realize the hierarchical processing of behavioral features. Finally, a student behavior prediction model is established based on the K-nearest neighbor nonparametric regression method, and the accuracy of the model behavior prediction is optimized by the TPE hyperparametric method. The AUC value of the model constructed in this paper for student behavior prediction reaches 0.813 on average, and the model validity is verified. There is a positive correlation between the time students stay in the building and their academic performance, and the predicted grades of students who spend more time in the building are in the range of 80-100. And there is no significant difference in academic behavior among students with different spending behaviors. This paper lays a foundation for accurate prediction of student behavior in colleges and universities, and provides a reference for college and university teaching administrators to make scientific management and decision-making.
The rapid development of social economy makes the intelligent management of colleges and universities more and more attention [1]. The times are progressing, and the management of colleges and universities should follow the progress in order to better serve the students [2]. Entering the era of big data, all walks of life produce a lot of data [3]. Schools form all kinds of information all the time, such as the daily consumption record of a card, students’ family information, personal basic information, etc. [4-5], and all kinds of data can refract the daily life of students. The database of colleges and universities with the superposition of time, its data more and more, together constitute a huge big data environment [6-7]. Based on this, it is very necessary for colleges and universities to analyze the data and dig deeper into the value of the data.
However, at present, the application of smart campus construction in domestic colleges and universities is still in the stage of continuous adjustment, the lack of a more comprehensive and automated operation process, the main aspects of the research are still mainly semi-automated data analysis, etc. [8-9], the ability to analyze student behavior and other data generated within the campus automatically is insufficient, but also need to be more proactive towards the application level to do in-depth development and research, application convenience, safety performance, socialized operation, etc. are all elements that need to be considered [10-11].
Student behavioral portrait under big data is mainly based on students’ learning data and life behavior data to portray students’ performance during school in a complete way, i.e., the process of describing students or groups through the visual or non-visualized data generated by students’ behaviors such as consumption, learning, and participation in activities during school [12]. Usually, it is in the form of using labels or phrases to reflect the individual characteristics of students, while group portrait refers to reflecting the characteristics of student groups by constructing a collection of student groups. Comprehensive behavioral portrait analysis of students can accurately understand the life behaviors and learning of college students in school from multiple angles, all-round and three-dimensional [13].
The results of data analysis of education and behavior, including conventional analysis and mining results, can provide new ideas for problems in the field of modernization of education, forcing the indicators of education methods, student management, education indicators, and other aspects to keep pace with the times.
Literature [14] expresses the importance of predicting students and that student behavior prediction is an important part of a smart campus, for example, predicting whether a student will fail to graduate can alert the student affairs office to take predictive measures to help students improve their academic performance. Literature [15] proposes a formal model of a student’s shared exercise process and its discovery from a student’s exercise log as well as several measures of similarity between an individual student’s exercise behavior and a student’s shared exercise process. Literature [16] suggests that modeling of students’ learning behaviors or preferences is considered an important indicator of their course grades, but few studies have used it to predict students’ online course grades. Literature [17] indicated that it is crucial to accurately present and predict students’ knowledge, and showed experimentally that the predictive accuracy of our method was extensively evaluated and explained on five large-scale datasets in different learning domains such as math, spelling learning, and physics. Literature [18] identified three main factors of individual environmental contexts, including social norms, policies and regulations, and facility support, through factor analysis based on survey data of Chinese residents. Literature [19] interweaves awareness, challenges and opportunities to demonstrate the value of big data. While recognizing the value of big data for business, there are challenges in data quality and usage. Literature [20] states that big data enables HR to analyze and predict and make smarter and more accurate decisions, and that the application of big data analytics by HR has a significant impact on talent management. Literature [21] states that student-led EMS has a practical educational effect on students, improves social evaluation of schools, and reduces environmental burdens.
In this paper, we use the constraints to construct the university student behavior data processing as a dataset, determine the Eps neighborhood of the student behavior characteristics by improving the initial center point of the DT-kmeans clustering algorithm, and then statistically calculate the density of the student behavior data and select the initial class cluster center point. Then calculate the Euclidean distance between each data and the center point, and iteratively update to get the final class cluster center point to realize the clustering analysis of student behavior characteristics. The entropy weight method is used to calculate the weight value of student behavioral characteristics and establish the hierarchical model of student behavioral characteristics. Finally, based on the K-nearest neighbor nonparametric regression method, the prediction model of student behavior in colleges and universities is constructed. After calculating the similarity between the target students’ behavioral features and the behavioral feature vectors of the near-neighbors, the behavior of the target students is obtained by predicting the behavior of the near-neighbors. Meanwhile, the TPE hyperparameter method is proposed to optimize the prediction model and improve the accuracy of the model in predicting student behavior. Finally, after analyzing the predictive validity of the model, the consumer behavior and spatio-temporal behavior of students in college A are clustered and the learning behavior of students with different clustering characteristics are predicted and analyzed to explore the application effect of the model.
In this paper, an improved K-means clustering algorithm DT-kmeans is proposed to optimize the selection of the initial centroids for cluster analysis of students’ behavioral characteristics.The DT-kmeans algorithm first determines the Eps neighborhood based on the t-nearest-neighbor distance, and then statistically counts the density information of the students’ behavioral data objects through the Eps neighborhood, and the algorithm randomly selects a certain data object of the students’ behavioral data set as the initial class cluster centroid. The algorithm randomly selects a data object in the student behavior data set as the initial cluster centroid, and the selection of the remaining cluster centroids will be based on both the density of the data object and the minimum distance between the data object and the already existing cluster centroids, and through the setting of the probability function, the data object that is both high-density and far away from the already existing cluster centroids will have a higher probability of being selected as the new cluster centroid.
The DT-Kmeans algorithm consists of the following steps in sequence.
Input the target dataset \(D\) containing \(n\) data object and the number of clusters to be clustered in the dataset \(k\).
Calculate the Euclidean distance between all data objects within the target student behavior dataset \(D\), and store the Euclidean distance information in the distance distribution matrix \(D_{n*n}\).
Calculate the Eps neighborhood parameter \(\eta\) based on the number of data objects contained in the student behavior dataset \(n\).
Based on the distance distribution matrix \(D_{n*n}\) of the dataset, take out the \(\eta\)th smallest distance parameter \(d\left(x_{i\eta } \right)\) in each row to get the distance array \(D_{\eta }\).
Based on the distance array \(D_{\eta }\), average the distance data in the array to obtain the neighborhood parameter Eps.
Count the density information of the student behavior data object, i.e., the number of data objects in the dataset whose Euclidean distance to the data object is less than or equal to the neighborhood parameter Eps.
Define an empty set \(T\) and place the data object information from student behavior data set \(D\) into set \(T\) with the density information of the corresponding data object.
Define an empty set \(V\) to hold the centroids of the student behavior class clusters.
Randomly select a data object from set \(T\) and put it into \(V\) as the initial cluster center point, and then remove the point from set \(T\).
Count the minimum value of the Euclidean distance between the student behavior data object in set \(T\) and the class cluster centroid in set \(V\).
Select a data object from the set of student behavioral characteristics \(T\) to be added to the set of class cluster centroids \(V\) as a new class cluster centroid. For data object \(t_{i}\) in set \(T\), determine the weight \(w\left(t_{j} \right)\) of being selected as the class cluster centroid, the probability that data object \(t_{i}\) is added is \(p=\frac{w\left(t_{j} \right)}{\sum _{t_{u\in T} }w \left(t_{u} \right)}\), and remove the data object from set \(T\) that was added to class cluster centroid set \(V\).
Repeat the iterative steps 10 and 11 until the number of data in set \(V\) is \(k\).
Participate in K-means clustering by using the student behavior data in set \(V\) obtained in step 12 as the initial class cluster centroids of the K-means clustering algorithm.
Calculate the distance between each data object in data set \(D\) and the \(k\) class cluster centroids, and assign the data objects to the class clusters represented by the class cluster centroids with the closest Euclidean distance.
Count the data object information in each class cluster, take the mean value as the new class cluster center point, and update the class cluster center point information.
Iteratively perform steps 14 and 15 until the center point of the algorithm class clusters no longer change.
Output clustering results, \(k\) independent of each other student behavior characteristics class clusters for \(C=\left\{C_{1} ,C_{2} ,\cdots ,C_{k} \right\}\).
In order to construct a hierarchical model of student behavior, different weights need to be assigned to different features in the set of student behavioral features formed above based on the DT-kmeans clustering algorithm in order to differentiate the extent to which the different features contribute to the model and satisfy: \[\label{GrindEQ__1_} \sum _{i=1}^{m}w_{i} =1.\tag{1}\]
Student behavioral characteristics represent, in varying degrees, indicators of student behavioral performance in school, and a weight is assigned to each characteristic to create a hierarchical model of student behavioral characteristics: \[\label{GrindEQ__2_} S_{i} =W_{i} C_{i} .\tag{2}\]
In order to establish a hierarchical model of students’ behavioral characteristics, this paper uses the entropy weight method to determine the weight of each student’s behavioral characteristics, which is obtained by processing the data through statistical methods. The behavioral characteristics of students are expressed as a \(n*m\)st order matrix \(X=\left(x_{ij} \right)_{m\cdot n}\), where \(x_{ij}\) represents the value of the \(j\)th behavioral characteristic of student \(i\). \(m\) represents the size of the dimension of the student’s behavioral characteristics. The calculation process of entropy weight method is as follows.
Form the original student behavior characteristics matrix: \[\label{GrindEQ__3_} X=\left(\begin{array}{ccc} {x_{11} } & {\ldots } & {x_{11} } \\ {\vdots } & {\ddots } & {\vdots } \\ {x_{1m} } & {\ldots } & {x_{11} } \end{array}\right) ,\tag{3}\] where is the value of the \(i\)nd evaluated student object under the \(j\)st indicator.
Normalization of the original student behavioral characteristics matrix is done as follows.
The larger the better type of indicator: \[\label{GrindEQ__4_} V_{ij} =\frac{x_{ij} -\min \left(x_{j} \right)}{\max \left(x_{j} \right)-\min \left(x_{j} \right)} .\tag{4}\]
The smaller the better type indicator: \[\label{GrindEQ__5_} V_{ij} =\frac{\max \left(x_{j} \right)-x_{ij} }{\max \left(x_{j} \right)-\min \left(x_{j} \right)} ,\tag{5}\] where, \(V_{ij}\) represents the value of the weight of the \(j\)rd student behavioral characteristic of student \(i\), \(\max \left(x_{j} \right)\) and \(\min \left(x_{j} \right)\) are the maximum and minimum values of the \({\rm j}\)th student behavioral characteristic value respectively.
Calculate the weight of the characteristics of the \(i\)th evaluation object under \(j\) indicators, and note the weight of the characteristics of the \(i\)th evaluation object under \(j\) indicators \(p_{ij}\), then: \[\label{GrindEQ__6_} p_{ij} =\frac{V_{ij} }{\sum _{i=1}^{m}V_{ij} } .\tag{6}\]
Calculate the entropy value of the \(j\)st student behavioral characteristic: \[\label{GrindEQ__7_} E_{j} =\frac{-1}{\ln m\sum _{i=1}^{m}p_{ij} \cdot \ln p_{ij} }.\tag{7}\]
Calculation of weights: \[\label{GrindEQ__8_} W_{j} =\frac{1-E_{j} }{\sum _{j=1}^{m}\left(1-E_{j} \right) }.\tag{8}\]
In this paper, the method of entropy right is introduced to objective empowerment. Therefore, this method evaluates the contribution of each time domain index to the result of clustering. Entropy is used to determine the disorder and information utility of the system. On the basis of the entropy right method, according to the information of the information, the entropy method adopts type (7) and (8), and a small entropy value represents a considerable information utility, which is therefore an important weight.
Based on the student behavior feature mining and stratification model proposed above, the specific flow of the constructed student behavior prediction model is shown in Figure 1. On the basis of the student behavior feature clustering and stratification model, the student grade level is determined based on the students’ personal information, and the sample of senior students participating in student behavior prediction is extracted accordingly. Then, the similarity between the target students and senior students is calculated based on the student behavior hierarchical model, and in order to improve the accuracy of the prediction effect, this paper standardizes the data before the behavioral similarity of the two students is calculated. Then, the K senior students who are closest or most similar to the target student \(x\) to be predicted are identified based on the similarity. Finally, based on the behavioral characteristics of these K near-neighboring seniors in the to-be-predicted semester, an indicator of the behavioral characteristics of the target student in the to-be-predicted semester is predicted based on nonparametric regression. The similarity between the target students and the students in the training sample set is calculated and reflected in this paper using weighted Euclidean distances, with smaller distances indicating greater similarity and vice versa.
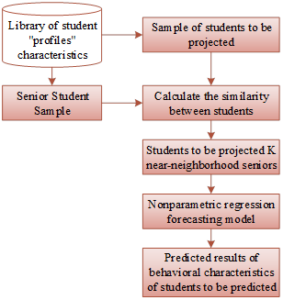
Assuming that the behavioral characteristics of all students are in a \(N\)-dimensional space and each student \(x\) is represented as a feature vector \(\left(a(x)_{1} ,a(x)_{2} ,\ldots ,a(x)_{n} \right)\), where \(a(x)_{r}\) denotes the eigenvalue of the \(r\)th feature attribute of student \(x\), then the similarity between two students \(x\), \(y\) is obtained based on the weighted distance, and the Euclidean distance formula is shown in (9): \[\label{GrindEQ__9_} sim(x,y)=\frac{1}{\sum _{i=1}^{n}\sqrt{\left(a(x)_{i} -a(x)_{j} \right)^{2} } } .\tag{9}\]
The Euclidean distance is added to the weight of each feature, and the weighted distance formula used in this paper is shown in (10): \[\label{GrindEQ__10_} d(x,y)=\sum _{i=1}^{m}\left(w_{i} \left(a(x)_{i} -a(x)_{j} \right)\right)^{2} .\tag{10}\] When \(\sum _{i=1}^{n}\sqrt{\left(a(x)_{i} -a(x)_{j} \right)^{2} }\) is replaced by \(\sum _{i=1}^{m}\big(w_{i} \big(a(x)_{i}\) \(-a(x)_{j} \big)\big)^{2}\) in the distance formula the similarity between the vectors will depend on the weights in Eq. Adjusting the weights will determine the importance of each attribute in the similarity computation, and appropriate weights greatly optimize the accuracy of our K-nearest neighbor students.
Then, a K-dimensional vector of student behavioral characteristics will be obtained for each dimension among the K near-neighbor students obtained above. \(\left(a_{1} ,a_{2} ,\ldots ,a_{k} \right)\) The traditional K-nearest-neighbor regression algorithm takes the average of the K near-neighbor samples as the predicted value of the prediction sample. In contrast, in this paper, by letting the role of the K student samples in the nearest neighbor on the prediction result be related to the distance from the target student, students closer to the target student have more influence on the prediction result and contribute more to the prediction result. For the student to be predicted \(x\), its K nearest neighbors \(\left(a_{1} ,a_{2} ,\ldots ,a_{k} \right)\), the distances between them and \(x\) are \(\left(D_{1} ,D_{2} ,\ldots ,D_{k} \right)\). The following conditions must be satisfied to define the prediction weight of each nearest neighbor student for \(x\).
The further the distance from the student to be predicted \(x\), the smaller the weight.
satisfies the normalization condition, i.e., \(\sum _{i=1}^{k}\omega _{i} =1\).
Because: \[ \label{GrindEQ__11_} \sum _{i=1}^{k}\omega _{i} =k-\frac{\sum _{i=1}^{k}D_{i} }{\sum _{i=1}^{k}D_{i} } -k\cdot \frac{k-2}{k}\] \[=\sum _{i=1}^{k}\left(1-\frac{D_{i} }{\sum _{i=1}^{k}D_{i} } -\frac{k-2}{k} \right). \tag{11} \]
For each nearest neighbor student \(i\), its prediction weight for \(x\) is defined as follows: \[\label{GrindEQ__12_} \omega _{i} =1-\frac{D_{i} }{\sum _{i=1}^{k}D_{i} } -\frac{k-2}{k} .\tag{12}\]
As a result, the student’s student behavior in the target semester can be predicted by the K-nearest senior, as shown in Eq: \[\label{GrindEQ__13_} a_{xj} =\sum _{i=1}^{k}\omega _{i} a_{ij},\tag{13}\] where, \(a_{ij}\) denotes the true value of student \(i\) in terms of behavioral characteristics \(j\) and \(a_{xj}\) denotes the predicted value of student \(x\) to be predicted in terms of \(j\) characteristics.
In this paper, the constructed student behavior prediction model is optimized using the TPE hyperparametric method.The TPE optimization algorithm is a sequential model-based optimization method with strong convergence and exploration ability, which can specialize and fine-tune the search for a certain optimal region.The TPE converts the hyperparametric space into a nonparametric density distribution for the process of modeling \(p(x|y)\). This conversion is done in three ways, specifically, as the uniform distribution is converted to a truncated Gaussian mixture, the logarithmic uniform distribution is converted to an exponential-phase Gaussian mixture, and the discrete distribution is converted to a reweighted discrete distribution.
The TPE optimization algorithm is processed by substituting different observations \(\left(x^{1} ,x^{2} ,\ldots ,x^{k} \right)\) in the nonparametric density, allowing the use of learning algorithms based on different densities. Its density is defined as: \[\label{GrindEQ__14_} p\left(x|y\right)=\left\{\begin{array}{ll} {l(x)} & {if{\rm \; }y<y^{*} } \\ {g(x)} & {if{\rm \; }y\ge y^{*} } \end{array}\right. ,\tag{14}\] where \(l(x)\) consists of densities where the objective function \(F(x)\) of observation \(\left\{x^{i} \right\}\) is less than \(y^{*}\) and \(g(x)\) consists of densities where the objective function \(F(x)\) of observation \(\left\{x^{i} \right\}\) is greater than or equal to \(y^{*}\). In general, the TPE uses \(y^{*}\) as the quantile \(\gamma\) for observation \(y\) By maintaining a ranked list of observations in the observation domain \(H\), the running time of the TPE optimization algorithm for each iteration can be scaled linearly in \(|H|\) and out of the optimized student behavioral profile dimensions, at which point the desired lift \((EI)\) is: \[ EI_{y^{*} } (x)=\int _{-\infty }^{\infty }\left(y^{*} -y\right) p(y|x)dy\] \[=\int _{-\infty }^{y^{*} }\left(y^{*} -y\right) \frac{p(x|y)p(y)}{p(x)} dy. \tag{15}\]
Finally, constructions \(\gamma ={\rm p}\left({\rm y}<y^{*} \right)\) and \(p(x)=\int p (x|y)p(y)dy=\gamma l(x)+(1-\gamma )g(x)\) can be obtained: \[\label{GrindEQ__16_} EI_{y^{*} } (x)=\left(r+\frac{g(x)}{l(x)} (1-\gamma )\right)^{-1} .\tag{16}\] Thus, each iteration returns a \(x^{*}\) that obtains the maximum \(EI\) value.
In this paper, we use campus behavioral data from two data sources (consumption data from Logistics Group and access control data from Security Office) to predict students’ behaviors by taking some time periods of data for experiments. Starting from March 1, 2023, data from 7, 14, 21, 28, and 35 days are intercepted as the training dataset to predict the behavior of students in the following 1 day. For example, for the 14-day dataset, the training set is the campus behavior data from March 1 to March 14, then the constructed student behavior prediction model has 14 network snapshots. Since some students may not be involved in the relevant behaviors during the selected time period, and some locations may be unvisited, which can lead to inconsistency in the number of nodes in the data of different time lengths, the detailed information of the five college student behavior datasets constructed is shown in Table 1. Although the behavior of college students on campus is cyclical, the number of growth per 7 days is also inconsistent, there is one significant increase in the number of people in the 3rd week of the school year, which should be a part of the students have just returned to school, but the growth of the number of behaviors in the first 3 weeks is more stable, in the 4th week (28 days) due to the number of behaviors of the students who have returned to school in the 3rd week in the 7-day period becomes more, compared to the number of behaviors of the previous week increases by 57,392, but In week 5 there is another 1 drop (14271), this is because at the beginning of week 5 is a longer vacation period, and some students may have left school again, which can also lead to a challenge in the task of predicting the behavior of students in colleges and universities.
| Time span | Number | ||||
|---|---|---|---|---|---|
| Node | Student | Train hyperlink | 7 days increases | Test hyperlink | |
| 7 days | 2148 | 1997 | 41596 | 41596 | 4992 |
| 14 days | 2254 | 2064 | 84571 | 42975 | 10149 |
| 21 days | 2596 | 2475 | 128962 | 34391 | 19075 |
| 28 days | 2682 | 2536 | 16354 | 57392 | 21162 |
| 35 days | 2671 | 2549 | 190625 | 14271 | 22875 |
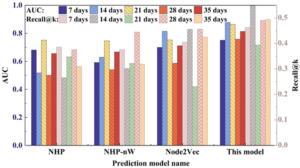
In order to verify the effectiveness of the behavior prediction model constructed in this paper on the task of student behavior prediction, it is compared with three school behavior prediction methods, namely, Node2Vec, NHP, and NHP-nW.The Node2Vec model is a commonly used network representation learning method. Since the Node2Vec algorithm cannot accomplish the task of hyperedge prediction, only the Node2Vec algorithm is used in this experiment to generate vector representations of nodes, and then the hyperedge interaction scoring module is trained to obtain the hyperedge prediction results.The NHP model is known to be the current optimal hyperedge prediction model, and since the NHP supports hyperedges with weights, the dense characteristics of the school behavioral data lead to the dynamic school behavioral As NHP supports hyperedge with weights, but the denser characteristics of campus behavior data lead to the dynamic campus behavior due to the higher connection density in the information network, which may lead to the deterioration of the effect of using the hyperedge with weights, the experimental process compares NHP with the version of NHP-W that does not consider the weights of the hyperedge, to validate the difference in the effect on different datasets. To ensure fairness, the hyperparameters selected by Node2Vec, NHP and the prediction model in this paper are kept consistent.
In this experiment, AUC and Recall@k score were used as the main evaluation indicators of the prediction effectiveness of the model. For all datasets, the test set is the data of one consecutive day after the training set, taking the 14-day dataset as an example, the student behavior from March 1 to March 14 is used as the training set to predict the possible behavior of students on March 15. Figure 2 shows the analysis results of AUC and Recall@k scores of Node2Vec, NHP, NHP-nW and the behavior prediction model in different training and test sets. On the contrary, the AUC evaluation index of the NHP-nW model in the 14-day dataset (0.629) and the 28-day dataset (0.541) exceeded that of the NHP model, and the effect of the NHP-W model was more stable than that of the NHP model, which may be due to the dense connections in the campus behavior data, and sometimes the removal of duplicate edges is more conducive to the model to obtain the hidden features in the data. According to the analysis results of the student behavior prediction model constructed in this paper, it is found that the model has the best effect in the 14-day dataset, with AUC and Recall@k reaching 0.878 and 0.567, respectively, and there is a certain decrease in the subsequent datasets. The prediction accuracy on the 21-day dataset decreased by 0.015 compared with the 14-day dataset, which may be due to a large increase in the number of students, and therefore the accuracy of the prediction results decreased. The results in the 28-day dataset may have been broken by the predicted day and the approach of a longer holiday, which led to a change in student behavior and a break in periodicity, so the Recall@k score dropped to 0.491. In the 35-day dataset, the students’ behavior during the May Day holiday was used for behavior prediction because of the model’s extraction of time series features, resulting in a relatively low result. Based on the comprehensive analysis results, the prediction model of student behavior in colleges and universities constructed in this paper is significantly better than that of the other three models due to the consideration of the dynamic and periodic characteristics of campus behavior data, and the prediction results of the five student behavior datasets are better. There is a good predictor of the behavior of students in different time periods.
The research data used in this section comes from 800 students in the third year of undergraduate studies in college A. The student behavior indicators are divided into two aspects: spatio-temporal behavior and consumption behavior, and two indicators, average monthly consumption and average single consumption, are selected to conduct a cluster analysis of students’ campus consumption using the DT-kmeans algorithm. Four indicators, namely, dormitory, teaching building, cafeteria and other locations, were selected to conduct cluster analysis of students’ spatio-temporal behavior. Finally, the clustering results are analyzed and illustrated and visualized.
Cluster analysis of consumer behavior.
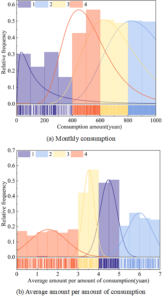
The DT-kmeans algorithm was used to cluster the students’ consumption data, and the specific clustering results of the students’ consumption data are shown in Figure 3 (a) and (b) are the clustering results of the students’ average monthly consumption and single consumption amount, respectively. The students were divided into four groups, the first group accounted for 26% of the total number of students, and the average monthly consumption of students was the lowest among all groups, ranging from 0 to 400 yuan, while the single consumption amount was high (4-5 yuan), indicating that such students did not often spend in school. The second group of students accounts for 18% of all students, and the average monthly consumption of this group of students is 800-1000 yuan, and the single consumption amount is between 5-7 yuan, indicating that this type of student has a high standard of living and sufficient living expenses. The average monthly consumption level of the third group of students (35%) is in the middle (600-800 yuan), and the single consumption amount is also medium (3-4 yuan). The fourth group of students accounted for 21%, and the average monthly consumption and single consumption amount were relatively low, indicating that such students were more active in school consumption, but their consumption level was limited and their lives were more frugal.
Spatio-temporal behavior cluster analysis.
According to the average length of time students spend in the dormitory, teaching building, cafeteria and other locations will be students’ spatio-temporal behavioral characteristics of the cluster analysis, spatio-temporal behavioral characteristics of the specific clustering analysis results are shown in Table 2, clustering there are three types of behavioral patterns of students. Category 1 is closed students (A), the number of students in this category is 365, and the location where the students with this behavioral pattern distribute their time the most is the dormitory, that is, on average, 56.48% of their time is spent in the dormitory, and less time is spent in the academic building, the cafeteria, and other locations. Students in category 2 are active (B), and from the clustering results it can be seen that there is no obvious prominent location for the distribution of students’ time. The time spent in dormitories, academic buildings, cafeterias, and other locations is relatively balanced, all in the range of 19%-22%. Even more time was spent in locations other than dormitories and academic buildings, with an average percentage of 38.4%. The 3rd category of students is the study type (C), and the location with the highest distribution of time for students with this behavioral pattern is the academic building, with a corresponding value of 59.74%. The time spent in the dormitory (16.98%) and in other locations (8.76%) were relatively low, and students of this type were more studious.
| Categories | Student population | Student proportion | Dormitory ratio | Teaching building | Canteen time ratio | Other location time ratio |
|---|---|---|---|---|---|---|
| A | 365 | 45.63% | 56.48% | 15.42% | 25.67% | 2.43% |
| B | 227 | 28.38% | 21.48% | 20.65% | 19.47% | 38.4% |
| C | 208 | 26.00% | 16.98% | 59.74% | 14.52% | 8.76% |
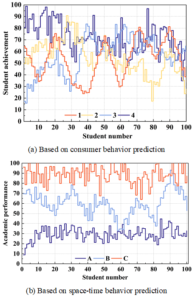
In this section, learning behavior prediction analyses are conducted for different types of students with different consumption behaviors and spatio-temporal behaviors respectively to explore the effects of different clustering characteristics on students’ academic performance. For different types of students in both consumption behavior clustering and spatio-temporal behavior clustering, 100 students are randomly selected for learning behavior prediction analysis. The results of students’ learning behavior prediction analysis obtained by using the behavioral prediction model are shown in Figure 4, (a) and (b) are the results of students’ learning performance for different consumption behaviors and spatio-temporal behaviors, respectively. From the results of learning behavior prediction, there is no obvious difference in the distribution of predicted grades among students with four different consumption behavior characteristics, indicating that the characteristic of consumption behavior does not have too much influence on students’ learning behavior. However, it can be seen that the predicted grades of students in category 1 are more variable, fluctuating between 20-80 points, indicating that teachers should pay attention to this type of students to prevent the occurrence of academic crisis situations. Most of the students in category 4 have scores between 60-100, probably due to poorer economic conditions, so they study harder, and more attention can be paid to this category of students in the selection of scholarships. The results of predicting academic performance based on spatio-temporal behavior showed significant differences in the performance of the three groups of students. There is a positive correlation between the time students stay in the building and their academic performance, with the predicted grades of most Type C students being in the range of 80-100, much higher than the 10-40 scores of Type A students. This indicates that most of the students with higher grades spend less time on average in the dormitory, while students with lower grades spend more time in the dormitory, and that college faculty can work on this area to improve students’ daily behaviors and improve their academic performance.
This paper proposes a behavioral feature stratification method based on clustering algorithm, and establishes a behavioral prediction model for college students based on K-nearest neighbor nonparametric regression method. The model prediction effectiveness and practical application effect are analyzed, and the results show that:
The prediction model of student behavior in colleges and universities constructed in this paper has achieved good results in the prediction of five student behavior datasets because it considers the dynamic and periodic characteristics of campus behavior data. The best results were obtained in the 14-day dataset of student behavior, with AUC and Recall@k reaching 0.878 and 0.567, respectively.
The clustering analysis of students’ consumption behavior divides students into four types, and the average monthly consumption level of students in group 3 is medium, and the amount of single consumption is also medium. There are three behavioral patterns of students after temporal behavior clustering, and the location with the highest temporal distribution of students in group 3 is the teaching building, corresponding to a value of 59.74%, and this type of students has a higher learning nature.
Most of the students in category 4 in the cluster analysis of consumer behavior have scores between 60-100, probably due to poorer economic conditions, and therefore study harder, and more attention can be paid to this type of students in the selection of scholarships. It is also found that there is a positive correlation between the time students stay in the academic building and their academic performance, and the predicted scores of type C students are between 80-100, which is much higher than that of type A students, which is between 10-40.
On the whole, the behavior prediction model of college students proposed in this paper has a high accuracy rate and its effect in practical application has been verified, which can be widely used in college student management to improve students’ bad behavior in time.
The 2022 project of higher education reform and innovation in Shanxi Province “The Construction of Talent Cultivation and Management System for ‘Major Enrollment and Major Diversion’ from the perspective of ”Three-Wide Education System” Taking the School of Mechanical Engineering, North university of china “(project number: J20220580).