
In the design of printed circuit boards (PCBs), routing is a critical step that affects their performance and quality. Traditional manual wiring methods are not only time-consuming and error-prone, but also difficult to meet the design requirements of modern high-density and high-performance circuit boards. In this paper, an automatic PCB routing strategy based on ant colony algorithm is investigated, aiming to improve the routing efficiency and quality. Ant colony algorithm, as a swarm intelligent optimisation algorithm, has better robustness and constraints and is suitable for solving complex wiring problems. In this paper, we focus on two common wiring requirements, equal-length wiring and differential pair wiring. For equal length cabling, each line is optimised to meet the length matching requirement by setting the maximum length value and minimum length value using the ant colony algorithm. For differential pair wiring, firstly, the equidistance of signal lines is ensured by the method of two ants walking at the same time, and then the length of the line is fine-tuned to ensure that the length of the two signal lines is the same. The experimental results show that the improved ant colony algorithm has strong convergence and optimisation ability under the constraints of equal-length wiring and differential pair wiring, which provides an effective solution for PCB automatic wiring.
The rinted Circuit Board (PCB), as an important part of the information technology industry, plays a vital role in modern society. With the continuous progress of electronic technology, PCB has been widely used in aerospace, medical, transport, agriculture and many other fields. Especially driven by the demand for high-frequency and high-rate data transmission, the performance requirements of PCBs are increasing. With the development of packaging technology and the increase of integration, the design of PCBs has become more complex and important [1,2]. In PCB design, wiring, as the last step of design, directly affects the performance and reliability of the board [3]. For example, the delay of high-speed signal transmission, signal interference, and power consumption need to be effectively addressed in the wiring stage [4].
In practice, design engineers are usually able to design circuit diagrams with complex functions, but when performing the actual wiring, manual wiring is not only inefficient but also prone to errors due to the complex and time-consuming wiring process. Especially in large-scale designs, manual wiring takes a lot of time and manpower, which increases the design cost. In addition, with the increase in board integration, the wiring requirements have become more diverse, such as differential pair wiring, length-matched wiring, and symmetric wiring [5,6]. Traditional wiring tools have been difficult to meet the needs of modern PCB design and lack effective solutions [7].
Since PCB wiring problems are NP-hard problems, they are difficult to be solved by traditional mathematical modelling and optimization methods [8]. In this context, swarm intelligence algorithms, as an emerging optimisation method, show the potential to solve complex wiring problems. Ant colony algorithm, as one of swarm intelligence algorithms, has better robustness and constraints, and is able to consider multiple constraints simultaneously in the wiring process and optimise the feasible solution through iteration [9,10].
Although ACO algorithms perform well in solving complex optimisation problems, they still face many challenges in PCB wiring applications. Firstly, the wiring process needs to consider a variety of constraints, such as wire length matching, interference minimisation and path shortening [11]. These constraints constrain each other and increase the complexity of the problem. Secondly, the ant colony algorithm is prone to fall into local optimal solutions and converge slowly when dealing with large-scale wiring problems [12]. In addition, modern PCB wiring needs to deal with a large number of signal lines, and the performance of the traditional ACO algorithm on large-scale problems has not been fully verified [13].
In practice, equal-length cabling and differential pair cabling are two common and challenging cabling requirements. Equal-length cabling requires that the length of the same set of signal lines be essentially the same to ensure the synchronisation and integrity of high-frequency signal transmission [14]. Differential pair wiring, on the other hand, requires two signal lines to be consistent in length and distance to improve the anti-interference ability and signal integrity [15]. How to improve the convergence speed of the algorithm and the quality of the solution while ensuring the equal-length wiring and differential-pair wiring is the difficulty of the current research.
Currently, research solutions for PCB wiring problems are divided into two main categories: methods based on traditional optimisation algorithms and methods based on intelligent optimisation algorithms. Although traditional optimisation algorithms such as the exhaustive method can find the globally optimal solution, their time complexity is often exponential and difficult to be applied in large-scale problems.The methods based on intelligent optimisation algorithms, such as genetic algorithms and particle swarm algorithms, are able to find an approximate optimal solution in a shorter period of time, but still suffer from the problems of local optimality and slow convergence when dealing with multi-constraint and large-scale problems [16].
In terms of isometric wiring, traditional methods mainly use greedy algorithms to extend shorter lines by snaking lines and so on. However, this method easily leads to the blocking of other lines and reduces the success rate of wiring [17].In terms of differential pair wiring, existing studies mainly focus on equidistant and length matching of lines, but less consideration is given to metrics such as path offset, resulting in poor wiring quality [18].
In this paper, an automatic PCB routing strategy based on ant colony algorithm is proposed, and an improved ant colony algorithm is designed to improve the efficiency and quality of routing for the needs of equal-length routing and differential pair routing. In equal-length wiring, this paper uses the ACO algorithm to optimise each line by setting the maximum length value and minimum length value to ensure the consistency of the line length.In differential pair wiring, equal spacing of the signal lines is first ensured by two ants walking at the same time, and then the line lengths are fine-tuned to ensure that both signal lines are the same length.
The improved ACO algorithm has the following advantages when dealing with multi-constraint and large-scale problems:
In the wiring process, multiple constraints such as line length matching, interference minimisation and path shortest are considered simultaneously to improve the quality of the solution through iterative optimisation.
Speed up the convergence of the algorithm by optimising the pheromone evaporation and updating mechanism to prevent falling into local optimal solutions.
In large-scale wiring problems, the improved ACO algorithm can effectively handle a large number of signal lines and improve the success rate and quality of wiring.
This paper experimentally verifies the effectiveness of the improved ant colony algorithm in isometric wiring and differential pair wiring, demonstrating the advantages of the algorithm in dealing with practical problems.
Due to the increased performance of current boards, it is often necessary to accomplish high frequency communications, making the control of clock frequencies more and more stringent. Especially when clock frequencies above gigahertz are used on boards, time constraints become very strict.The signal delay is often due to mismatch of wire lengths, which is one of the most important causes of circuit performance. Typically, the delay of a circuit is proportional to the length of the wire, and control of the delay can be converted to control of the wire length, hence the need for equal-length wiring on devices with high clock frequencies.As shown in Figure 1, this wiring method needs to ensure that the lengths of the wires within a set of wire networks are basically the same or the maximum length error is small, and this is one of the important needs of the current high-frequency circuit board wiring.
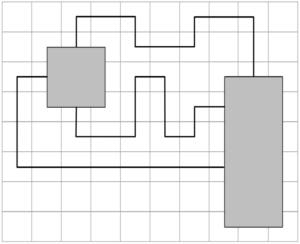
Equal-length wiring, which can also be referred to as length-matched wiring, is mainly accomplished by placing certain constraints on the length of the line; the constraints are mainly classified into two cases, which are maximum-minimum length constraints and finite-length difference constraints.
The ant colony algorithm has a positive feedback mechanism that can work with the pheromone of ants to constrain the objective. In the case of isometric wiring, the difference in length within the line network can be used as an optimisation objective to achieve the result of consistent lengths for each line.During path selection, the difference between the current line length and the target length will be used to judge whether a detour is needed to satisfy the line length constraint, but a detour that is too large may cause the current line to occupy the area of other lines in the same line network, forcing the other lines to detour again.In order to prevent other ants from occupying all the key nodes of certain lines, randomly selected endpoints of equidistant lines are used in this algorithm for layout as a way to increase the success rate of the line network layout.
The isometric lines can be completed in two phases when they are laid out, firstly in the first phase the shortest line lengths are wired for each line, taking the maximum and minimum of all line lengths in the current line network as the primary constraints, and the shortest total line lengths as the secondary constraints.Then in the second stage, to speed up the convergence of the algorithm, the pheromone at the end of the first stage is used as the initial value of the current ant pheromone. Using \({\tau _{\min }}\) and \({\tau _{\max }}\) as boundaries, half of the pheromone on each side is volatilised to prevent the algorithm from converging too quickly making the feasible solution of poor quality.The final value is set as the target length value, which corrects the length of each end line in the current line network, and is updated when the algorithm converges to prevent the length of the current longest line from being exceeded. When updating the pheromone in the second stage, the current line length should be made to converge quickly to the vicinity of the specified line length, so the pheromone increment for each side is calculated as shown in Eq. (1).
\[\label{e1} \Delta \tau_{i j}=\left\{\frac{Q}{a b s\left(\frac{L_{b e s t}-\operatorname{maxLen}}{0}\right)} \frac{i f(i, f) \in \text { current optimal path }}{\text { otherwise }}\right..\tag{1}\]
Since the isometric line network is composed of multiple sets of two-ended line networks, the basic idea of two-ended wiring can be borrowed. In the first stage, the end condition of a single iteration is that all the two-end contour lines in the current line network are wired through, and the smallest feasible solution is selected as the current optimal solution after several iterations. In the second stage, the main focus is to expand the line length less than the isometric line.
In the isometric wiring, can be divided into two stages of wiring, in the current isometric wire mesh group all the two ends of the wire through the case of a group of wire lengths will be obtained. Then take the maximum value of this group as the base value, correct the rest of the line length, and update the line length base value in real time to ensure that the final value of all line lengths are basically the same.In this experiment the base value of the line length is used as the target condition, in order to verify that the improved ant colony algorithm has strong constraints for this type of problem, the value of the line length after each iteration is recorded, and the convergence graph of the line length correction is plotted as well as the final wiring effect.
Figure2 shows the correction convergence diagram and wiring effect diagram of the first group of equal length lines. A total of three equal length lines need to be arranged in this network group. After the first stage of wiring, the values of each wire length are 129, 137, and 115, with a maximum value of 137. Therefore, 137 is used as the initial reference value for layout. Figure 3 shows the correction convergence diagram and wiring effect diagram of the second group of equal length lines. There are a total of five equal length lines that need to be arranged in this network group. After the completion of the first stage layout, the lengths of each line are 120, 126, 132, 138, 144, and the maximum value of 144 is selected as the initial benchmark value for equal length lines.
As can be seen from the figure, when the line length benchmark value is determined, the rest of the line length that does not meet the value will be quickly adjusted and converge to the benchmark line length, in order to achieve the basic consistency of the line length in the line network group. It is shown that updating the pheromone with different objective values as constraints can directly affect the final convergence result of the algorithm to satisfy the effect of improving the ant colony algorithm with stronger constraints.
Differential signal lines are very common in high-speed circuit board design, such as USB, HDMI and Ethernet for data transmission are wired as differential pairs. Differential pairs have good immunity to electromagnetic interference, and each pair of differential lines carries signals of the same size and in opposite directions, which are transmitted along a channel .Since the signal lines are in close proximity, noise on the channel is absorbed by both signals at the same time. When wiring differential pairs, it is necessary to consider matching the lengths of the two lines as a way to improve the performance and signal integrity of the circuit. Usually, when arranging differential signal lines, length matching is used for close wiring. Figure 4 illustrates the wiring intent of a pair of differential signal transmission lines, from which it can be seen that the differential signal lines remain equally spaced and close together in length.
Single-ended signal lines are used to transmit signals with one signal line and one ground line, and the voltage amplitude may change during transmission due to external influences.When the signal reaches the opposite end, the difference between the size of the signal and the ground will change, which is not the same as when it was sent, resulting in the opposite end not being able to receive the correct signal, so the transmission method has poor anti-interference capability.
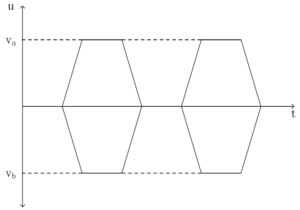
The signal transmission waveform on the differential signal line is shown in Figure 5, where \({v_a} = – {v_b}\). From the graph, it can be seen that at any time, the voltage on both signal lines is the same, and the direction is opposite. The voltage difference between the two transmission lines is \(v = {v_a} – {v_b} = 2{v_a}\). If external interference causes the voltage on the differential signal line to shift at a certain moment, with an amplitude of t , then the voltage difference between the two transmission lines is \(v = ({v_a} + \Delta v) – ({v_b} + \Delta v) = 2{v_a}\). This voltage difference is the same as the difference without interference, indicating that the differential signal line has a suppressive effect on noise with appropriate offset.From a signal integrity point of view, differential signals can suppress crosstalk, synchronous switching noise, power supply noise, and ground plane bounce noise.
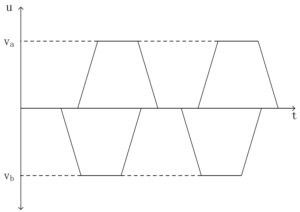
After arranging the differential signal lines, it is necessary to judge whether the two line lengths are the same. If the line lengths are not equal then equal length processing is performed, otherwise there will be a time delay during signal transmission and the phase on the longer signal line will be shifted back, as shown in Figure 6. If the transmission of two signal lines cannot be unified in terms of timing, it will cause a change in the voltage difference on the line, which will prevent the receiving end from obtaining the correct signal.
The wiring of differential pairs using ACO algorithm can be done in two steps, the first step is to consider only the requirement of equidistance so that two ants walk at the same time and the second step is to satisfy the requirement of line length.In the first step, the adjacency finding method needs to be adjusted so that each time the next step of the line is performed, the two ants move together, and its purpose is to constrain the two signal lines to be strictly equidistant. In the second step it is necessary to fine-tune the line length on the basis of the first step wiring to ensure that the line length is consistent.
When carrying out the first step of isometric wiring, all the steps are the same as the two-end wiring, except for the search method of neighbouring points. According to the current walking direction of the ants to judge the next reachable point, and then use the selection probability formula for state selection, if the current ants search for the end point or the next reachable point is empty then stop searching.The algorithm still requires several iterations, and during each iteration, each pair of ants is given a set of feasible solutions, but only the solution with the optimal path among them needs to be chosen as the result of this iteration.Since the spacing constraints of the two ants have been ensured during the neighbourhood pathfinding process, the minimum path length difference between the two ants is first taken as the primary goal in the subsequent selection. When the path length difference is consistent then the requirements such as line length and number of inflection points are constrained separately, and the pheromone is updated after each iteration to prepare for the next iteration.
The ants can be divided into two cases when searching for neighbouring points, straight or cornering, for straight points it is straightforward to judge whether the next point in the current direction is feasible or not, if it is unreachable then the neighbouring point is dropped, otherwise it is added to the neighbouring point vector.For the adjacent points that need to turn, the judgment is based on the specific situation. In Figure 7, the eight situations where ants turn are illustrated using images. The turning methods are divided into bottom right, top right, bottom left, top left, top right, top left, bottom left, and bottom right based on the current direction and the direction to be reached. When turning, take the current position of one ant as the origin, and the other ant explores the path.Firstly, determine whether the position where the circle is located in the figure is feasible or not, if it is feasible, then it means that the ants are allowed to make a turn in the current direction and add the point after the turn to the neighbouring point vector, otherwise, they should give up travelling away from that direction.
After completing the equidistant wiring, there exists a line between each of the two starting points and the target point, but the lengths of these two lines are not necessarily the same. Line expansion is required to achieve equal length in differential pair wiring, so the shorter line is mainly corrected in the second step of differential pair wiring.In the process of correcting a line, it is inevitable that fluctuations in the line will need to occur, thus destroying the equidistance constraints, so it is often desirable that the line being expanded is less distant from the original line, a problem that can be measured using the path offset degree.
Path offset is used to measure the deviation between the expanded path and the current path, and can control the trajectory of the expanded route to be as consistent as possible with the original route. As shown in Figure 8, Line1 is the original line, Line2 is the expanded line, and \({t_1}\) and \({t_2}\) respectively represent the size of the area blocks that the expanded line deviates from the original line.The path offset is the sum of the squares of the sizes of these area blocks, for example, the path offset of Line 2 relative to Line 1 is \(t = t_1^2 + t_2^2\). The purpose of adding square operations to each offset block is to prevent the existence of large offset blocks and to make the expanded line as close as possible to the original line.When using the improved ACO algorithm for the second wiring step, the line length difference should be used as the first constraint and the path deviation as the second constraint. When the path deviation is small, it means that the corrected line is basically the same spacing as the other signal line, because the original line is perfectly equidistant from the other signal line.Thus correcting for line length in the case of equidistant can be converted to controlling the line length of the current path as well as the degree of offset from the original path to satisfy the requirements of differential pair wiring.

The following experiment shows two sets of differential pair routing, one group does not require line length correction, while the other group requires line length correction, to demonstrate the rationality of the algorithm design. Figure 9 shows the wiring effect of two sets of differential signal lines, where Figure 9 does not require length matching processing, and the line length and distance are completely consistent at the end of the first step of wiring.it is not possible to find a set of lines that have exactly the same length, so the second step of length matching processing is needed. From the graph, it can be seen that ants make small fluctuations around the original line, thereby achieving the effect of extending the line.

In this paper, a PCB auto-routing strategy based on improved ant colony algorithm is proposed, and an optimisation scheme is designed and experimentally verified for the requirements of equal-length routing and differential pair routing.Through an in-depth analysis of the specific needs of isochronous and differential pairs of cabling, this paper investigates how to improve the efficiency and quality of cabling while meeting these needs. The following are the main conclusions of this paper’s research:
The improved ant colony algorithm proposed in this paper performs well in dealing with PCB wiring problems with multiple constraints. By optimising the pheromone volatility and updating mechanism, the convergence speed and global search ability of the algorithm are improved, and the problem of falling into local optimal solutions is effectively avoided. The experimental results show that the improved ACO algorithm achieves significant performance improvement in both equal-length wiring and differential pair wiring tasks.
The wiring strategy studied in this paper is able to handle multiple constraints simultaneously, including line length matching, interference minimisation and path shortest. By setting the maximum length value and minimum length value, and optimising each line using the ant colony algorithm, this paper effectively achieves the requirement of equal length wiring. In terms of differential pair wiring, the equidistant and length-matched signal lines are ensured by the method of synchronous walking of double ants, thus improving the integrity and anti-interference capability of signal transmission.
Through experimental verification of multiple PCB design examples, the improved ant colony algorithm proposed in this paper performs better than traditional methods in both equal length routing and differential pair routing tasks. The experimental results show that the improved ant colony algorithm significantly improves the success rate and quality of routing when dealing with large-scale routing problems, fully demonstrating its feasibility and effectiveness in practical applications.
Although the research in this paper has achieved remarkable results, there are still some issues that deserve further exploration. Future research directions include further optimising the parameter settings and pheromone updating mechanism of the ant colony algorithm, and improving the convergence speed and quality of the algorithm. Research more adaptable routing algorithms for larger and more complex PCB designs to meet the challenges in real engineering. Develop more comprehensive optimisation algorithms by introducing more constraints and optimisation objectives in the routing process, such as power consumption, signal integrity and thermal management.Combining the Ant Colony algorithm with other intelligent optimisation algorithms (e.g. Genetic Algorithm, Particle Swarm Algorithm, etc.) and exploring the application of Hybrid Optimisation Methods to improve the efficiency and quality of wiring.