
Chemical graph theory is prominent research area in mathematical chemistry, due to its extensive applications especially in quantitative structure-activity relationships (QSARs) where eccentricity based topological invariants are used for the mathematical modeling of biological activities of molecules, identifying structurally similar molecules and used to study the structure and properties of materials, such as polymers and ceramics. Carbon nanotubes (CNTs) are cylindrical structures made up of carbon atoms that are arranged in a unique hexagonal pattern. In this research, we examine the \(NA^{n}_{m}\) nanotube after considering it in the form of chemical graph and compute eccentricity based topological invariants like eccentric-connectivity index with total-eccentricity index with some versions of the zagreb indices.
Mathematical chemistry is a field of study that involves the application of mathematical models, methods, and algorithms to describe and understand chemical phenomena. It combines mathematical principles with chemistry to develop theories, models, and computational tools to analyze chemical systems and predict their behavior. Chemical graph theory is a subfield of mathematical chemistry that studies the mathematical properties of molecular structures represented as graphs. In chemical graph theory, a molecule is represented as a graph, where atoms are represented as nodes, and bonds between atoms are represented as edges. Chemical graph theory gives numerous essential methods for the evaluation of chemical structures. For chemical compounds the prediction of the biological activities and properties the QSAR and QSPR relationships are applicable significantly. In chemical graph theory some mathematical and computational methods are utilized at atomic level for evaluation of the chemical structures [1],[2]. Chemical graph theory has applications in various fields, such as drug discovery, materials science, and catalysis. It is an essential tool for understanding and designing new molecules and materials, as well as for predicting their properties and behavior.
A graph \(G=(V,E)\) contains \(V\) as a set of vertices and \(E\) as a set of edges, where \(G\) is undirected graph without multiple edges and loops. The vertices adjacent with \(u\) is its degree denoted by \(d(u)\). A walk in \(G\) is a sequence of adjacent vertices where a walk without vertex repetition is called a path. Distance is a shortest path between the pair of vertices denoted by \(d(u,v)\) [3]. Eccentricity is the distance between \(u\) and a vertex that is farthest from \(u\) denoted by \(\varepsilon(u)\) [3]-[5].
The representation of a graph by a matrix, polynomial, sequence or a numerical quantity has essential features in graph theory. The numerical value of a graph which identify its topology called topological index or graph invariant. A number is called a topological index of a graph \(G\) denoted by \(Top(G)\) with the property for two isomorphic graphs \(H\) and \(G\), we have \(Top(H) = Top(G)\). Topological indices in organic chemistry are very helpful for the structure activity relationships, structure property relationships, isomer discrimination, chemical documentation and pharmaceutical drug design. There are several degree-based, distance and eccentricity based graph invariants. Especially eccentricity based topological invariants are useful for the mathematical modeling of several biological activities of molecules of diverse nature. Eccentricity based topological invariants have been shown to be effective in identifying structurally similar molecules, which can be useful in drug design and discovery. Also Eccentricity-based topological indices have been used to study the structure and properties of materials, such as polymers and ceramics. These indices can provide insight into the bonding and electronic properties of these materials, which can be useful in designing new materials with specific properties. [6],[7].

Concept of topological indices started from Wiener index, which is half sum of the distances divided by \(2\) between all pairs of vertices [8], given by,
\[\label{eq1} W(G)=\frac{1}{2}\sum\limits_{(u,v)}d(u,v). \tag{1}\]
Eccentric connectivity index is a distance-based topological index was presented by Sharma, Goswami, and Madan [9],[10]. As compared to Wiener index, eccentric connectivity index shows greater order predictability and high discriminating power from structure property and structure activity [11]. The mathematical expression is, \[\label{eq2} \xi(G) = \sum\limits_{u\in V(G)}[d(u)\epsilon(u)]. \tag{2}\] Total-eccentricity index is obtained when the vertex degree is not considered [12]-[14]. The mathematical expression is, \[\label{eq3} \varsigma(G) = \sum\limits_{u\in V(G)} [\epsilon(u)]. \tag{3}\]
Zagreb indices with their variants are very useful in the studies of QSPR and QSAR. Vukičeivc and Graovac presented Zagreb eccentricity indices [15]. Also Modjtaba Ghorbani, Mohammad A. Hosseinzadeh stated the new version of Zagreb indices [16],[17]. The first, second and third zagreb eccentricity indices are described as [18]-[20],
\[\ M_1^*(G) = \sum\limits_{uv\in E(G)} [\epsilon(u) + \epsilon(v)], \tag{4}\] \[\ M_1^{**}(G) = \sum\limits_{v\in V(G)} [\epsilon(v)]^2, \tag{5}\] \[\ M_2^*(G) = \sum\limits_{uv\in E(G)} [\epsilon(u)\epsilon(v)]. \tag{6}\]
For more detailed study on eccentricity based topological indices see [21].
Carbon nanotubes (CNTs) are cylindrical structures made up of carbon atoms that are arranged in a unique hexagonal pattern shown in Fig.1. They are a type of nanomaterial with remarkable mechanical, electrical, and thermal properties, which make them attractive for a wide range of applications, including electronics, energy storage, and materials science. In this research we consider a carbon nanotube in the form of a sheet.
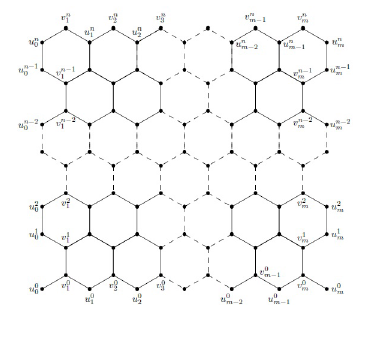
Let the quadrilateral section \(P^{n}_{m}\) with dimensions \(m\times n\). We have \(n\geq 2\) hexagons on lateral side with \(m\geq 2\) hexagons on upper and lower sides. In Figure.2 the hexagonal lattice \(L\) is shown. Consider the vertices \(u^{j}_{0}\) and \(u^{j}_{m}\) by identifying two lateral sides of \(P^{n}_{m}\) by taking \({j=\lbrace 0,1,2,…,n}\rbrace\), we acquire \(NA^{n}_{m}\).
In our research, let \(NA^{n}_{m}\) in replacement of \(P^{n}_{m}\) with \(n=m\), we compute eccentric connectivity index with total-eccentricity index and some Zagreb eccentricity indices for various cases.
In this section we discuss our main results.
Theorem 1. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 0(mod 2)\). The eccentric-connectivity index is,
\(\xi(G)=10n+\sum\limits_{m=1}^{\frac{n}{2},n>2}(6nt-2mt)+\sum\limits_{m=\frac{n}{2}}^{n,n>2}(4nt+2mt)+\sum\limits_{m=0}\left[\sum\limits_{k=2}^{n-2,n>2}(6nt-2mt-2kt-12n+4m+4k)\right]+\sum\limits_{m=1}^{\frac{n}{2}}\left[\sum\limits_{k\equiv 0(mod 2)}^{n}(\frac{9}{2}nt^{2}-\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-\frac{9}{2}nt+\frac{3}{2}mt+\frac{3}{2}kt)\right]+\sum\limits_{m=\frac{n}{2}}^{n}\left[\sum\limits_{k\equiv 0(mod 2)}^{n}(3nt^{2}+\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-2nt-\frac{3}{2}mt+\frac{3}{2}kt)\right]+\sum\limits_{m=0}^{\frac{n}{2}}\left[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(\frac{9}{2}nt^{2}-\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}+9nt-3mt-3kt)\right]+\sum\limits_{m=\frac{n}{2}}^{n-1}\left[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(3nt^{2}+\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-6nt-3mt-3kt)\right]+\sum\limits_{m\equiv 0(mod 2)}\left[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(4nt+2mt-2kt)\right]+46.\)
Proof. Let \(G\cong NA^{n}_{m}\). From Eq. (2), we have, \[\xi(G)=\sum\limits_{u\in V(G)}[d(u)\epsilon(u)].\]
By utilizing Table 1 in Eq. (2), we get,
\(\xi(G)=1\times 2\times 3n+2\times 2\times 5+2\times t\times \sum\limits_{m=1,t\neq2}^{\frac{n}{2},n>2}(3n-m)+2\times 2\times 6+2\times t\times \sum\limits_{m=\frac{n}{2},t\neq2}^{n,n>2}(2n+m)+2\times (t-2)\times \sum\limits_{m=0}\sum\limits_{k\equiv 0(mod 2)}^{n-2,n>2}(3n-m-k)+3\times \frac{t^{2}-t}{2}\times \sum\limits_{m=1}^{\frac{n}{2}}\sum\limits_{k\equiv 0(mod 2)}^{n}(3n-m-k)+3\times \frac{t^{2}-t}{2}\times \sum\limits_{m=\frac{n}{2}}^{n}\sum\limits_{k\equiv 0(mod 2)}^{n}(2n+m-k)+2\times 1\times (2n+1)+(3)\times (\frac{t^{2}+2t}{2}\times \sum\limits_{m=0}^{\frac{n}{2}}\sum\limits_{k\equiv 1(mod 2)}^{n-1}(3n-m-k))+3\times \frac{t^{2}-2t}{2}\times \sum\limits_{m=\frac{n}{2}}^{n-1}\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2n+m-k)+2\times t\times \sum\limits_{m\equiv 0(mod 2)}\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2n+m-k).\)
After simplification, we get
\(\xi(G)=10n+\sum\limits_{m=1}^{\frac{n}{2},n>2}(6nt-2mt)+\sum\limits_{m=\frac{n}{2}}^{n,n>2}(4nt+2mt)+\sum\limits_{m=0}[\sum\limits_{k=2}^{n-2,n>2}(6nt-2mt-2kt-12n+4m+4k)]+\sum\limits_{m=1}^{\frac{n}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n}(\frac{9}{2}nt^{2}-\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-\frac{9}{2}nt+\frac{3}{2}mt+\frac{3}{2}kt)]+\sum\limits_{m=\frac{n}{2}}^{n}[\sum\limits_{k\equiv 0(mod 2)}^{n}(3nt^{2}+\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-2nt-\frac{3}{2}mt+\frac{3}{2}kt)]+\sum\limits_{m=0}^{\frac{n}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(\frac{9}{2}nt^{2}-\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}+9nt-3mt-3kt)]+\sum\limits_{m=\frac{n}{2}}^{n-1}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}\\(3nt^{2}+\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-6nt-3mt-3kt)]+\sum\limits_{m\equiv 0(mod 2)}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(4nt+2mt-2kt)]+46.\) ◻
Theorem 2. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 1(mod 2)\). The eccentric-connectivity index is,
\(\xi(G)=12n+\sum\limits_{m=1}^{\frac{n-1}{2}}(6nt-2mt-6n+2m)+\sum\limits_{m=\frac{n+1}{2}}^{n-1}(4nt+2mt-4n-2m)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(6nt-2mt-2kt-6n+2m+2k)]+\sum\limits_{m=n}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(4nt+2mt-2kt-4n-2m+2k)]+\sum\limits_{m=1}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(\frac{9}{2}nt^{2}-\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-9nt+3mt+3kt+\frac{9}{2}n-\frac{3}{2}m-\frac{3}{2}k)]+\sum\limits_{m=\frac{n+1}{2}}^{n-1}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3nt^{2}+\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-6nt-3mt+3kt+3n+\frac{3}{2}m-\frac{3}{2}k)]+\sum\limits_{m=0}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n}(\frac{9}{2}nt^{2}-\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}+\frac{9}{2}nt-\frac{3}{2}mt-\frac{3}{2}kt)]+\sum\limits_{m=\frac{n+1}{n}}^{n}[\sum\limits_{k\equiv 1(mod 2)}^{n}(3nt^{2}+\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}+3nt+\frac{3}{2}mt-\frac{3}{2}kt)].\)
Proof. Let \(G\cong NA^{n}_{m}\). From Eq. (2), we have, \[\xi(G)=\sum\limits_{u\in V(G)}[d(u)\epsilon(u)].\]
By utilizing Table 2 in Eq. (2), we get,
\(\xi(G)=1\times 4\times 3n+2\times \frac{2t-2}{2}\times \sum\limits_{m=1}^{\frac{n-1}{2}}(3n-m)+\frac{2t-2}{2}\times 2\times \sum\limits_{m=\frac{n+1}{2}}^{n-1}(2n+m)+(t-1)\times 2\times \sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3n-m-k)]+(t-1)\times 2\times \sum\limits_{m=n}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2n+m-k)]+3\times \frac{t^{2}-2t+1}{2}\times \sum\limits_{m=1}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3n-m-k)]+3\times \frac{t^{2}-2t+1}{2}\times \sum\limits_{m=\frac{n+1}{2}}^{n-1}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2n+m-k)]+3\times \frac{t^{2}+t}{2}\times \sum\limits_{m=0}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n}(3n-m-k)]+3\times \frac{t^{2}+t}{2}\times \sum\limits_{m=\frac{n+1}{2}}^{n}[\sum\limits_{k\equiv 1(mod 2)}^{n}(2n+m-k)].\)
After simplification, we get,
\(\xi(G)=12n+\sum\limits_{m=1}^{\frac{n-1}{2}}(6nt-2mt-6n+2m)+\sum\limits_{m=\frac{n+1}{2}}^{n-1}(4nt+2mt-4n-2m)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(6nt-2mt-2kt-6n+2m+2k)]+\sum\limits_{m=n}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(4nt+2mt-2kt-4n-2m+2k)]+\sum\limits_{m=1}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(\frac{9}{2}nt^{2}-\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-9nt+3mt+3kt+\frac{9}{2}n-\frac{3}{2}m-\frac{3}{2}k)]+\sum\limits_{m=\frac{n+1}{2}}^{n-1}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3nt^{2}+\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}-6nt-3mt+3kt+3n+\frac{3}{2}m-\frac{3}{2}k)]+\sum\limits_{m=0}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n}(\frac{9}{2}nt^{2}-\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}+\frac{9}{2}nt-\frac{3}{2}mt-\frac{3}{2}kt)]+\sum\limits_{m=\frac{n+1}{n}}^{n}[\sum\limits_{k\equiv 1(mod 2)}^{n}(3nt^{2}+\frac{3}{2}mt^{2}-\frac{3}{2}kt^{2}+3nt+\frac{3}{2}mt-\frac{3}{2}kt)].\) ◻
| \(\text{Representatives}\) | \(\text{Degree}\) | \(\text{Eccentricity}\) | \(\text{Range}\) | \(\text{Frequency}\) |
| {\(u_i^m,u_n-i^m\)} | \(3\) | \((3n-m-k)\) | \((1\leq m \leq \frac{n}{2})\), | \( \frac{t^{2}-t}{2}\), |
| \((1\leq i \leq \frac{n}{2})\) \(\forall\) \(m\), | ||||
| \((2\leq k \leq n)\) | \(t\) is even. | |||
| \(k\) is even. \(\forall\) \(m\). | ||||
| {\(u_i^m,u_n-i^m\)} | \(2\) | \((2n+m)\) | \(\lbrace m=2\), \( n=2\rbrace\), | \(t\), |
| \((\frac{n}{2}\leq m \leq n)\), \( n>2\), | \(t\) is even. | |||
| \(\lbrace i=0\rbrace\). | \( t\neq 2\). | |||
| {\(u_i^m,u_n-i^m\)} | \(3\) | \((2n+m-k)\) | \((\frac{n}{2}\leq m \leq n)\) | \(\frac{t^{2}-t}{2}\), |
| \((1\leq i \leq \frac{n}{2})\) \(\forall\) \(m\), | ||||
| \((2 \leq k \leq n)\), | \(t\) is even. | |||
| \(k\) is even. \(\forall\) m. | ||||
| {\(u_\frac{n}{2}^0\)} | \(2\) | \((2n+1)\) | \(\lbrace m=0, n\equiv 0(mod 2)\rbrace\) | \(1\) |
| {\(v_i^m,v_n-i+1^m\)} | \(3\) | \((3n-m-k)\) | \((0\leq m \leq \frac{n}{2})\), | \(\frac{t^{2}+2t}{2}\), |
| \((1\leq i \leq \frac{n}{2})\) \(\forall\) \(m\), | ||||
| \((1\leq k \leq n-1)\), | \(t\) is even. | |||
| \(k\) is even. \(\forall\) m. | ||||
| {\(u_i^m,u_n-i^m\)} | \(1\) | \((3n)\) | \(\lbrace i=0\) , | \(2\) |
| \( m=0\rbrace\). | ||||
| {\(u_i^0,u_n-i^0\)} | \(2\) | \((3n-m-k)\) | \(\lbrace m=0\rbrace\), | \(t-2\), |
| \((2\leq k \leq n-2,n\neq 2)\) | ||||
| \(k\) is even. | \(t\) is even. | |||
| \((1\leq i \leq \frac{n}{2}-1, n\neq 2)\). | ||||
| {\(v_i^m,v_n-i+1^m\)} | \(3\) | \((2n+m-k)\) | \((\frac{n}{2}\leq m \leq n-1)\), | \(\frac{t^{2}-2t}{2}\), |
| \((1\leq i \leq \frac{n}{2})\) \(\forall\) \(m\), | ||||
| \((1\leq k \leq n-1)\), | \(t\) is even. | |||
| \(k\) is odd. \(\forall\) \(m\). | ||||
| {\(u_i^m,u_n-i^m\)} | \(2\) | \((3n-m)\) | \(\lbrace m=1 \rbrace\), \(\lbrace n=2 \rbrace\), | \(t\), |
| \((1\leq m \leq \frac{n}{2})\) \(\lbrace n>2\rbrace\), | \(t\) is even. | |||
| \(\lbrace i=0\rbrace\). | \( t\neq 2\). | |||
| {\(v_i^m,v_n-i+1^m\)} | \(2\) | \((2n+m-k)\) | \(\lbrace m=n\equiv 0(mod 2)\rbrace\) | \(t,\) |
| \((1\leq i \leq \frac{n}{2})\) \(\forall\) \(m\) , | ||||
| \((1\leq k \leq n-1)\), | \(t\) is even. | |||
| \(k\) is odd. \(\forall\) \(m\). |
| \(\text{Representatives}\) | \(\text{Degree}\) | \(\text{Eccentricity}\) | \(\text{Range}\) | \(\text{Frequency}\) |
| {\(u_i^m,u_n-i^m\)} | \(1\) | \((3n)\) | \(\lbrace m=0, m=n\rbrace\), \(\lbrace i=0\rbrace\) | \(4\) |
| {\(u_i^m,u_n-i^m\)} | \(2\) | \((3n-m)\) | \((1 \leq m \leq \frac{n-1}{2})\) , | \(\frac{2t-2}{2}\), |
| \(\lbrace i=0\rbrace, \forall m\) | \(t\) is odd. | |||
| {\(u_i^m,u_n-i^m\)} | \(3\) | \((3n-m-k)\) | \((1\leq m \leq \frac{n-1}{2})\), | \(\frac{t^{2}-2t+1}{2}\), |
| \((1\leq i \leq \frac{n-1}{2})\) \(\forall\) \(m\), | ||||
| \((2\leq k \leq n-1)\) \(\forall\) \(m\), | \(t\) is odd. | |||
| \(k\) is even. | ||||
| {\(u_i^0,u_n-i^0\)} | \(2\) | \((3n-m-k)\) | \(\lbrace m=0\rbrace\), | \(t-1\), |
| \((1\leq i \leq \frac{n-1}{2})\) \(\forall\) \(m\), | ||||
| \((2\leq k \leq n-1)\) \(\forall\) \(m\), | \(t\) is odd. | |||
| \(k\) is even. | ||||
| {\(u_i^m,u_n-i^m\)} | \(2\) | \((2n+m)\) | \((\frac{n+1}{2}\leq m \leq n-1)\), | \(\frac{2t-2}{2}\), |
| \(\lbrace i=0\rbrace\), \(\forall\) m | \(t\) is odd. | |||
| . | ||||
| {\(v_i^m,v_n-i+1^m\)} | \(3\) | \((3n-m-k)\) | \((0\leq m \leq \frac{n-1}{2})\), | \(\frac{t^{2}+t}{2}\), |
| \((1\leq i \leq \frac{n+1}{2})\) \(\forall\) \(m\), | ||||
| \((1\leq k \leq n)\) \(\forall\) \(m\), | \(t\) is odd. | |||
| \(k\) is odd. | ||||
| {\(u_i^m,u_n-i^m\)} | \(3\) | \((2n+m-k)\) | \((\frac{n+1}{2}\leq m \leq n-1)\), | \(\frac{t^{2}-2t+1}{2}\), |
| \((1\leq i \leq \frac{n-1}{2})\) \(\forall\) \(m\), | ||||
| \((2\leq k \leq n-1)\) \(\forall\) \(m\), | \(t\) is odd. | |||
| \(k\) is even. | ||||
| {\(v_i^m,v_n-i+1^m\)} | \(3\) | \((2n+m-k)\) | \((\frac{n+1}{2}\leq m \leq n)\), | \(\frac{t^{2}+t}{2}\), |
| \((1\leq i \leq \frac{n+1}{2})\) \(\forall\) \(m\), | ||||
| \((1\leq k \leq n)\) \(\forall\) \(m\), | \(t\) is odd. | |||
| \(k\) is odd. | ||||
| {\(u_i^m,u_n-i^m\)} | \(2\) | \((2n+m-k)\) | \(\lbrace m=n\rbrace\), | \(t-1\), |
| \((1\leq i \leq \frac{n-1}{2})\) \(\forall\) \(m\), | ||||
| \((2\leq k \leq n-1)\) \(\forall\) \(m\), | \(t\) is odd. | |||
| \(k\) is even. |
Theorem 3. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 0(mod 2)\), then total-eccentricity index is,
\(\varsigma(G)=8n+\sum\limits_{m=1}^{\frac{n}{2},n>2}(3nt-mt)+\sum\limits_{m=\frac{n}{2}}^{n,n>2}(2nt+mt)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-2}(3nt-mt-kt-6n+2m+2k)]+\sum\limits_{m=1}^{\frac{n}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n}(\frac{3}{2}nt^{2}-\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-\frac{3}{2}nt+\frac{1}{2}mt+\frac{1}{2}mk)]+\sum\limits_{m=\frac{n}{2}}^{n}[\sum\limits_{k\equiv 0(mod 2)}^{n}(nt^{2}+\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-nt-\frac{1}{2}mt+\frac{1}{2}kt)]+\sum\limits_{m=0}^{\frac{n}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(\frac{3}{2}nt^{2}-\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}+3nt-mt-kt)]+\sum\limits_{m=\frac{n}{2}}^{n-1}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(nt^{2}+\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-2nt-mt+kt)]+\sum\limits_{m\equiv 0(mod 2)}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2nt+mt-kt)]+23.\)
Proof. Let \(G\cong NA^{n}_{m}\). Then from Eq. (3), we have, \[\varsigma(G)=\sum\limits_{u\in V(G)}\epsilon(u).\]
By utilizing Table 1 into Eq. (2), we get,
\(\varsigma(G)=2\times 3n+2\times 5+t\times \sum\limits_{m=1}^{\frac{n}{2},n>2}(3n-m)+6\times 2+t\times \sum\limits_{m=\frac{n}{2}}^{n,n>2}(2n+m)+(t-2)\times \sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-2}(3n-m-k)]+\frac{t^{2}-t}{2}\times (\sum\limits_{m=1}^{\frac{n}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n}(3n-m-k)])+\frac{t^{2}-t}{2}\times \sum\limits_{m=\frac{n}{2}}^{n}[\sum\limits_{k\equiv 0(mod 2)}^{n}(2n+m-k)]+2n\times 1+1+\frac{t^{2}+2t}{2}\times \sum\limits_{m=0}^{\frac{n}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(3n-m-k)]+\frac{t^{2}-2t}{2}\times \sum\limits_{m=\frac{n}{2}}^{n-1}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2n+m-k)]+t\times \sum\limits_{m\equiv 0(mod 2)}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2n+m-k)].\)
After simplification, we get
\(\varsigma(G)=8n+\sum\limits_{m=1}^{\frac{n}{2},n>2}(3nt-mt)+\sum\limits_{m=\frac{n}{2}}^{n,n>2}(2nt+mt)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-2}(3nt-mt-kt-6n+2m+2k)]+\sum\limits_{m=1}^{\frac{n}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n}(\frac{3}{2}nt^{2}-\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-\frac{3}{2}nt+\frac{1}{2}mt+\frac{1}{2}mk)]+\sum\limits_{m=\frac{n}{2}}^{n}[\sum\limits_{k\equiv 0(mod 2)}^{n}(nt^{2}+\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-nt-\frac{1}{2}mt+\frac{1}{2}kt)]+\sum\limits_{m=0}^{\frac{n}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(\frac{3}{2}nt^{2}-\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}+3nt-mt-kt)]+\sum\limits_{m=\frac{n}{2}}^{n-1}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(nt^{2}+\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-2nt-mt+kt)]+\sum\limits_{m\equiv 0(mod 2)}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2nt+mt-kt)]+23.\) ◻
Theorem 4. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 1(mod 2)\), then total-eccentricity index is,
\(\varsigma(G)=12n+\sum\limits_{m=1}^{\frac{n-1}{2}}(3nt-mt-3n+m)+\sum\limits_{m=\frac{n+1}{2}}^{n-1}(2nt+mt-2n-m)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3nt-mt-kt-3n+m+k)]+\sum\limits_{m=n}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2nt+mt-kt-2n-m+k)]+\sum\limits_{m=1}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(\frac{3}{2}nt^{2}-\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-3nt+mt+kt+\frac{3}{2}n-\frac{1}{2}m-\frac{1}{2}k)]+\sum\limits_{m=\frac{n+1}{2}}^{n-1}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(nt^{2}+\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-2nt-mt+kt+n+\frac{1}{2}m-\frac{1}{2}k)]+\sum\limits_{m=0}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n}(\frac{3}{2}nt^{2}-\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}+\frac{3}{2}nt-\frac{1}{2}mt-\frac{1}{2}kt)]+\sum\limits_{m=\frac{n+1}{2}}^{n}[\sum\limits_{k\equiv 1(mod 2)}^{n}(nt^{2}+\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}+nt+\frac{1}{2}mt-\frac{1}{2}kt)].\)
Proof. Let \(G\cong NA^{n}_{m}\). Then from Eq. (3), we have, \[\varsigma(G)=\sum\limits_{u\in V(G)}\epsilon(u)\] By utilizing Table 2 into Eq. (2), we get,
\(\varsigma(G)=4\times 3n+\frac{2t-2}{2}\times \sum\limits_{m=1}^{\frac{n-1}{2}}(3n-m)+\frac{2t-2}{2}\times \sum\limits_{m=\frac{n+1}{2}}^{n-1}(2n+m)+(t-1)\times \sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3n-m-k)]+(t-1)\times \sum\limits_{m=n}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2n+m-k)]+(\frac{t^{2}-2t+1}{2})\times \sum\limits_{m=1}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3n-m-k)]+\frac{t^{2}-2t+1}{2}\times \sum\limits_{m=\frac{n+1}{2}}^{n-1}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2n+m-k)]+\frac{t^{2}+t}{2}\times \sum\limits_{m=0}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n}(3n-m-k)]+(\frac{t^{2}+t}{2})\times \sum\limits_{m=\frac{n+1}{2}}^{n}[\sum\limits_{k\equiv 1(mod 2)}^{n}(2n+m-k)].\)
After simplification, we get,
\(\varsigma(G)=12n+\sum\limits_{m=1}^{\frac{n-1}{2}}(3nt-mt-3n+m)+\sum\limits_{m=\frac{n+1}{2}}^{n-1}(2nt+mt-2n-m)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3nt-mt-kt-3n+m+k)]+\sum\limits_{m=n}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2nt+mt-kt-2n-m+k)]+\sum\limits_{m=1}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(\frac{3}{2}nt^{2}-\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-3nt+mt+kt+\frac{3}{2}n-\frac{1}{2}m-\frac{1}{2}k)]+\sum\limits_{m=\frac{n+1}{2}}^{n-1}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(nt^{2}+\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}-2nt-mt+kt+n+\frac{1}{2}m-\frac{1}{2}k)]+\sum\limits_{m=0}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n}(\frac{3}{2}nt^{2}-\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}+\frac{3}{2}nt-\frac{1}{2}mt-\frac{1}{2}kt)]+\sum\limits_{m=\frac{n+1}{2}}^{n}[\sum\limits_{k\equiv 1(mod 2)}^{n}(nt^{2}+\frac{1}{2}mt^{2}-\frac{1}{2}kt^{2}+nt+\frac{1}{2}mt-\frac{1}{2}kt)].\) ◻
Theorem 5. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 0(mod 2)\). The first Zagreb-eccentricity index is,
\(M_{1}^{*}(G)=\sum\limits_{i=1}^{\frac{n}{2}}\sum\limits_{p=2n-\frac{n}{2}}^{2n-1}(12ip+6i-6p-3)+\sum\limits_{p=n\equiv 0(mod 2)}(12np+3n)+\sum\limits_{p=n\equiv 0(mod 2)}(8p+4)+\sum\limits_{i=\frac{n}{2}+3}(\frac{n}{2}-1)\underbrace{times}(6i-16)\times \sum\limits_{p=2n+1}^{3n-\frac{n}{2}-1}(2p+1)+\sum\limits_{i=3n+6j,0\leq j \leq \frac{n}{2}-1}\sum\limits_{p=3n-\frac{n}{2}}^{3n-1}(12np+6n-2ip-i).\)
Proof. Let \(G\cong NA^{n}_{m}\). From Eq. (4), we have, \[M_{1}^{*}(G)=\sum\limits_{uv\in E(G)}[\epsilon(u)+\epsilon(v)].\]
By utilizing Table 3, we get,
\(M_{1}^{*}(G)=\sum\limits_{i=1}^{\frac{n}{2}}(6i-3)\times \sum\limits_{p=2n-\frac{n}{2}}^{2n-1}(p+p+1)+3n\times \sum\limits_{p=n\equiv 0(mod 2)}(2p+2p+1)+2\times \sum\limits_{p=n\equiv 0(mod 2)}(2p+1+2p+1)+\sum\limits_{i=\frac{n}{2}+3}(\frac{n}{2}-1)\underbrace{times}(6i-16)\times \sum\limits_{p=2n+1}^{3n-\frac{n}{2}-1}(p+p+1)+\sum\limits_{i=3n+6j,0\leq j \leq \frac{n}{2}-1}\times \sum\limits_{p=3n-\frac{n}{2}}^{3n-1}(p+p+1).\)
After simplification, we get
\(M_{1}^{*}(G)=\sum\limits_{i=1}^{\frac{n}{2}}\sum\limits_{p=2n-\frac{n}{2}}^{2n-1}(12ip+6i-6p-3)+\sum\limits_{p=n\equiv 0(mod 2)}(12np+3n)+\sum\limits_{p=n\equiv 0(mod 2)}(8p+4)+\sum\limits_{i=\frac{n}{2}+3}(\frac{n}{2}-1)\underbrace{times}(6i-16)\times \sum\limits_{p=2n+1}^{3n-\frac{n}{2}-1}(2p+1)+\sum\limits_{i=3n+6j,0\leq j \leq \frac{n}{2}-1}\sum\limits_{p=3n-\frac{n}{2}}^{3n-1}(12np+6n-2ip-i).\) ◻
Theorem 6. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 1(mod 4)\). The first Zagreb-eccentricity index is,
\(M_{1}^{*}(G)=\sum\limits_{p=\frac{3n+1}{2}}(2p)+\sum\limits_{i=(\frac{n-1}{2})\underbrace{times}2}\sum\limits_{p=\frac{3n+1}{2}}^{\frac{5n-1}{2},p\equiv 0(mod 2)}(2ip)+\sum\limits_{i=1}^{\frac{n-3}{2},i\equiv 1(mod 2)}\sum\limits_{p=\frac{3n+1}{2}}^{2n-2, p\equiv 0(mod 2)}(8ip+4i)+\sum\limits_{i=2}^{\frac{n-1}{2}, i\equiv 0(mod 2)}\sum\limits_{p=\frac{3n+3}{2}}^{2n-1, p\equiv 1(mod 2)}(16ip+8i-4p-2)+\sum\limits_{i=2n+2}(\frac{n+3}{4})\underbrace{times}i\times \sum\limits_{p=2n}^{\frac{5n-1}{2}, p\equiv 0(mod 2)}(2p+1)+\sum\limits_{i=4n}(\frac{n-1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-3}{2}, p\equiv 1(mod 2)}(2p+1)+\sum\limits_{i=\frac{n-1}{4}}^{1}\sum\limits_{p=\frac{5n+1}{2}}^{3n-2, p\equiv 1(mod 2)}(32ip+16i)+\sum\limits_{i=\frac{n-3}{2}}^{1, i\equiv 1(mod 2)}\sum\limits_{p=\frac{5n+3}{2}}^{3n-1, p\equiv 0(mod 2)}(8ip+4i).\)
Proof. Let \(G\cong NA^{n}_{m}\) . From Eq. (4), we have, \[M_{1}^{*}(G)=\sum\limits_{uv\in E(G)}[\epsilon(u)+\epsilon(v)]\]
By utilizing Table 4, we get,
\(M_{1}^{*}(G)=1\times \sum\limits_{p=\frac{3n+1}{2}}(p+p)+\sum\limits_{i=(\frac{n-1}{2})\underbrace{times}2}i\times \sum\limits_{p=\frac{3n+1}{2}}^{\frac{5n-1}{2},p\equiv 0(mod 2)}(p+p)+\sum\limits_{i=1}^{\frac{n-3}{2},i\equiv 1(mod 2)}4i\times sum_{p=\frac{3n+1}{2}}^{2n-2, p\equiv 0(mod 2)}(p+p+1)+\sum\limits_{i=2}^{\frac{n-1}{2}, i\equiv 0(mod 2)}(8i-2)\times \sum\limits_{p=\frac{3n+3}{2}}^{2n-1, p\equiv 1(mod 2)}(p+p+1)+\sum\limits_{i=2n+2}(\frac{n+3}{4})\underbrace{times}i\times \sum\limits_{p=2n}^{\frac{5n-1}{2}, p\equiv 0(mod 2)}(p+p+1)+\sum\limits_{i=4n}(\frac{n-1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-3}{2}, p\equiv 1(mod 2)}(p+p+1)+\sum\limits_{i=\frac{n-1}{4}}^{1}16i\times \sum\limits_{p=\frac{5n+1}{2}}^{3n-2, p\equiv 1(mod 2)} (p+p+1)+\sum\limits_{i=\frac{n-3}{2}}^{1, i\equiv 1(mod 2)}4i\times \sum\limits_{p=\frac{5n+3}{2}}^{3n-1, p\equiv 0(mod 2)}(p+p+1).\)
After simplification, we get
\(M_{1}^{*}(G)=\sum\limits_{p=\frac{3n+1}{2}}(2p)+\sum\limits_{i=(\frac{n-1}{2})\underbrace{times}2}\sum\limits_{p=\frac{3n+1}{2}}^{\frac{5n-1}{2},p\equiv 0(mod 2)}(2ip)+\sum\limits_{i=1}^{\frac{n-3}{2},i\equiv 1(mod 2)}\sum\limits_{p=\frac{3n+1}{2}}^{2n-2, p\equiv 0(mod 2)}(8ip+4i)+\sum\limits_{i=2}^{\frac{n-1}{2}, i\equiv 0(mod 2)}\sum\limits_{p=\frac{3n+3}{2}}^{2n-1, p\equiv 1(mod 2)}(16ip+8i-4p-2)+\sum\limits_{i=2n+2}(\frac{n+3}{4})\underbrace{times}i\times \sum\limits_{p=2n}^{\frac{5n-1}{2}, p\equiv 0(mod 2)}(2p+1)+\sum\limits_{i=4n}(\frac{n-1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-3}{2}, p\equiv 1(mod 2)}(2p+1)+\sum\limits_{i=\frac{n-1}{4}}^{1}\sum\limits_{p=\frac{5n+1}{2}}^{3n-2, p\equiv 1(mod 2)}(32ip+16i)+\sum\limits_{i=\frac{n-3}{2}}^{1, i\equiv 1(mod 2)}\sum\limits_{p=\frac{5n+3}{2}}^{3n-1, p\equiv 0(mod 2)}(8ip+4i).\) ◻
Theorem 7. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 3(mod 4)\). The first Zagreb-eccentricity index is,
\(M_{1}^{*}(G)=\sum\limits_{i=(\frac{n+1}{2})\underbrace{times}2}\sum\limits_{p=\frac{3n+3}{2}}^{\frac{5n+1}{2}, p\equiv 0(mod 2)}(2ip)+\sum\limits_{i=1}^{\frac{n+1}{4}}\sum\limits_{p=\frac{3n+1}{2}}^{2n-1, p\equiv 1(mod 2)}(32ip+16i-20p-10)+\sum\limits_{i=1}^{\frac{n+1}{4}}\sum\limits_{p=\frac{3n+3}{2}}^{2n, p\equiv 0(mod 2)}(16ip+8i)+\sum\limits_{i=4n}(\frac{n+1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-1}{2}, p\equiv 1(mod 2)}(2p+1)+\sum\limits_{i=2n+2, n\neq 3}(\frac{n-3}{4})\underbrace{times}i\times \sum\limits_{p=2n+2, n\neq 3}^{\frac{5n-3}{2}, p\equiv 0(mod 2)}(2p+1)+\sum\limits_{i=1, n\neq 3}^{\frac{n-3}{4}}\sum\limits_{p=\frac{5n+3}{2}, n\neq 3}^{3n-2, p\equiv 1(mod 2)}(32ip+16i)+\sum\limits_{i=\frac{n+1}{4}}^{1}\sum\limits_{p=\frac{5n+1}{2}}^{3n-1, p\equiv 0(mod 2)}(16ip+8i-8p-4).\)
Proof. Let \(G\cong NA^{n}_{m}\). From Eq. (4), we have \[M_{1}^{*}(G)=\sum\limits_{uv\in E(G)}[\epsilon(u)+\epsilon(v)].\]
By utilizing Table 5, we get,
\(M_{1}^{*}(G)=\sum\limits_{i=(\frac{n+1}{2})\underbrace{times}2}i\times \sum\limits_{p=\frac{3n+3}{2}}^{\frac{5n+1}{2}, p\equiv 0(mod 2)}(p+p)+\sum\limits_{i=1}^{\frac{n+1}{4}}(16i-10)\times \sum\limits_{p=\frac{3n+1}{2}}^{2n-1, p\equiv 1(mod 2)}(p+p+1)+\sum\limits_{i=1}^{\frac{n+1}{4}}8i\times \sum\limits_{p=\frac{3n+3}{2}}^{2n, p\equiv 0(mod 2)}(p+p+1)+\sum\limits_{i=4n}(\frac{n+1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-1}{2}, p\equiv 1(mod 2)}(p+p+1)+\sum\limits_{i=2n+2, n\neq 3}(\frac{n-3}{4})\underbrace{times}i\times \sum\limits_{p=2n+2, n\neq 3}^{\frac{5n-3}{2}, p\equiv 0(mod 2)}(p+p+1)+\sum\limits_{i=1, n\neq 3}^{\frac{n-3}{4}}16i\times \sum\limits_{p=\frac{5n+3}{2}, n\neq 3}^{3n-2, p\equiv 1(mod 2)}(p+p+1)+\sum\limits_{i=\frac{n+1}{4}}^{1}(8i-4)\times \sum\limits_{p=\frac{5n+1}{2}}^{3n-1, p\equiv 0(mod 2)}(p+p+1).\)
After simplification, we get
\(M_{1}^{*}(G)=\sum\limits_{i=(\frac{n+1}{2})\underbrace{times}2}\sum\limits_{p=\frac{3n+3}{2}}^{\frac{5n+1}{2}, p\equiv 0(mod 2)}(2ip)+\sum\limits_{i=1}^{\frac{n+1}{4}}\sum\limits_{p=\frac{3n+1}{2}}^{2n-1, p\equiv 1(mod 2)}(32ip+16i-20p-10)+\sum\limits_{i=1}^{\frac{n+1}{4}}\sum\limits_{p=\frac{3n+3}{2}}^{2n, p\equiv 0(mod 2)}(16ip+8i)+\sum\limits_{i=4n}(\frac{n+1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-1}{2}, p\equiv 1(mod 2)}(2p+1)+\sum\limits_{i=2n+2, n\neq 3}(\frac{n-3}{4})\underbrace{times}i\times \sum\limits_{p=2n+2, n\neq 3}^{\frac{5n-3}{2}, p\equiv 0(mod 2)}(2p+1)+\sum\limits_{i=1, n\neq 3}^{\frac{n-3}{4}}\sum\limits_{p=\frac{5n+3}{2}, n\neq 3}^{3n-2, p\equiv 1(mod 2)}(32ip+16i)+\sum\limits_{i=\frac{n+1}{4}}^{1}\sum\limits_{p=\frac{5n+1}{2}}^{3n-1, p\equiv 0(mod 2)}(16ip+8i-8p-4).\) ◻
Theorem 8. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 0(mod 2)\). The second Zagreb-eccentricity index is,
\(M_{1}^{**}(G)=22n^{2}+4n+\sum\limits_{m=1}^{\frac{n}{2},n>2}(9n^{2}t+m^{2}t-6nmt)+\sum\limits_{m=\frac{n}{2}}^{n,n>2}(4n^{2}t+m^{2}t+4nmt)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-2,n>2}(9n^{2}t+m^{2}t+k^{2}t-6nmt+2mkt-6nkt-18n^{2}-2m^{2}-2k^{2}+12nm-4mk+12nk)]+\sum\limits_{m=1}^{\frac{n}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n}(\frac{9}{2}n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}-3nmt^{2}+mkt^{2}-3nkt^{2}-\frac{9}{2}n^{2}t-\frac{1}{2}m^{2}t-\frac{1}{2}k^{2}t+3nmt-mkt+3nkt)+\sum\limits_{m=\frac{n}{2}}^{n}[\sum\limits_{k\equiv 0(mod 2)}^{n}(2n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}+2nmt^{2}-mkt^{2}-2nkt^{2}-2n^{2}t-\frac{1}{2}m^{2}t-\frac{1}{2}k^{2}t-2nmt+mkt+2nkt)]+\sum\limits_{m=0}^{\frac{n}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(\frac{9}{2}n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}-3nmt^{2}+mkt^{2}-3nkt^{2}+9n^{2}t+m^{2}t+k^{2}t-6nmt+2mkt-6nkt)]+\sum\limits_{m=\frac{n}{2}}^{n-1}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}+2nmt^{2}-mkt^{2}-2nkt^{2}-4n^{2}t-m^{2}t-k^{2}t-4nmt+2mkt+4nkt)]+\sum\limits_{m\equiv 0(mod 2)}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(4n^{2}t+m^{2}t+k^{2}t+4nmt-2mkt-4nkt)]+123.\)
Proof. Let \(G\cong NA^{n}_{m}\). From Eq. (5), we have, \[M_{1}^{**}(G)=\sum\limits_{v\in V(G)}[\epsilon(v)]^{2}.\]
By utilizing Table 1, we get,
\(M_{1}^{**}(G)=2\times (3n)^{2}+2\times (5)^{2}+t\times \sum\limits_{m=1}^{\frac{n}{2},n>2}(3n-m)^{2}+2\times (6)^{2}+t\times \sum\limits_{m=\frac{n}{2}}^{n,n>2}(2n+m)^{2}+(t-2)\times \sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-2,n>2}(3n-m-k)^{2}]+(\frac{t^{2}-t}{2})\times \sum\limits_{m=1}^{\frac{n}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n}(3n-m-k)^{2}+\frac{t^{2}-t}{2}\times \sum\limits_{m=\frac{n}{2}}^{n}[\sum\limits_{k\equiv 0(mod 2)}^{n}(2n+m-k)^{2}]+(1)\times \sum\limits_{n\equiv 0(mod 2)}(2n+1)^{2}+\frac{t^{2}+2t}{2}\times \sum\limits_{m=0}^{\frac{n}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(3n-m-k)^{2}]+\frac{t^{2}-2t}{2}\times \sum\limits_{m=\frac{n}{2}}^{n-1}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2n+m-k)^{2}]+t\times \sum\limits_{m\equiv 0(mod 2)}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2n+m-k)^{2}].\)
After simplification, we get,
\(M_{1}^{**}(G)=22n^{2}+4n+\sum\limits_{m=1}^{\frac{n}{2},n>2}(9n^{2}t+m^{2}t-6nmt)+\sum\limits_{m=\frac{n}{2}}^{n,n>2}(4n^{2}t+m^{2}t+4nmt)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-2,n>2}(9n^{2}t+m^{2}t+k^{2}t-6nmt+2mkt-6nkt-18n^{2}-2m^{2}-2k^{2}+12nm-4mk+12nk)]+\sum\limits_{m=1}^{\frac{n}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n}(\frac{9}{2}n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}-3nmt^{2}+mkt^{2}-3nkt^{2}-\frac{9}{2}n^{2}t-\frac{1}{2}m^{2}t-\frac{1}{2}k^{2}t+3nmt-mkt+3nkt)+\sum\limits_{m=\frac{n}{2}}^{n}[\sum\limits_{k\equiv 0(mod 2)}^{n}(2n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}+2nmt^{2}-mkt^{2}-2nkt^{2}-2n^{2}t-\frac{1}{2}m^{2}t-\frac{1}{2}k^{2}t-2nmt+mkt+2nkt)]+\sum\limits_{m=0}^{\frac{n}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(\frac{9}{2}n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}-3nmt^{2}+mkt^{2}-3nkt^{2}+9n^{2}t+m^{2}t+k^{2}t-6nmt+2mkt-6nkt)]+\sum\limits_{m=\frac{n}{2}}^{n-1}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(2n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}+2nmt^{2}-mkt^{2}-2nkt^{2}-4n^{2}t-m^{2}t-k^{2}t-4nmt+2mkt+4nkt)]+\sum\limits_{m\equiv 0(mod 2)}[\sum\limits_{k\equiv 1(mod 2)}^{n-1}(4n^{2}t+m^{2}t+k^{2}t+4nmt-2mkt-4nkt)]+123.\) ◻
Theorem 9. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 1(mod 2)\). The second Zagreb-eccentricity index is,
\(M_{1}^{**}(G)=36n^{2}+\sum\limits_{m=1}^{\frac{n-1}{2}}(9n^{2}t+m^{2}t-6nmt-9n^{2}-m^{2}+6nm)+\sum\limits_{m=\frac{n+1}{2}}^{n-1}(4n^{2}t+m^{2}t+4nmt-4n^{2}-m^{2}-4nm)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(9n^{2}t+m^{2}t+k^{2}t-6nmt+2mkt-6nkt-9n^{2}-m^{2}-k^{2}+6nm-2mk+6nk)]+\sum\limits_{m=n}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(4n^{2}t+m^{2}t+k^{2}t+4nmt-2mkt-4nkt-4n^{2}-m^{2}-k^{2}-4nm+2mk+4nk)]+\sum\limits_{m=1}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(\frac{9}{2}n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}-3nmt^{2}+mkt^{2}-3nkt^{2}-9n^{2}t-m^{2}t-k^{2}t+6nmt-2mkt+6nkt+\frac{9}{2}n^{2}+\frac{1}{2}m^{2}+\frac{1}{2}k^{2}-3nm+mk-3nk)]+\sum\limits_{m=\frac{n+1}{2}}^{n-1}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}+2nmt^{2}-mkt^{2}-2nkt^{2}-4n^{2}t-m^{2}t-k^{2}t-4nmt+2mkt+4nkt+2n^{2}+\frac{1}{2}m^{2}+\frac{1}{2}k^{2}+2nm-mk-2nk)]+\sum\limits_{m=0}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n}(\frac{9}{2}n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}-3nmt^{2}+mkt^{2}-3nkt^{2}+\frac{9}{2}n^{2}t+\frac{1}{2}m^{2}t+\frac{1}{2}k^{2}t-3nmt+mkt-3nkt)]+\sum\limits_{m=\frac{n+1}{2}}^{n}[\sum\limits_{k\equiv 1(mod 2)}^{n}(2n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}+2nmt^{2}-mkt^{2}-2nkt^{2}+2n^{2}t+\frac{1}{2}m^{2}t+\frac{1}{2}k^{2}t+2nmt-mkt-2nkt)].\)
Proof. Let \(G\cong NA^{n}_{m}\). From Eq. (5), we have, \[M_{1}^{**}(G)=\sum\limits_{v\in V(G)}[\epsilon(v)]^{2}.\]
By utilizing Table 2, we get,
\(M_{1}^{**}(G)=4\times (3n)^{2}+\frac{2t-2}{2}\times \sum\limits_{m=1}^{\frac{n-1}{2}}(3n-m)^{2}+\frac{2t-2}{2}\times \sum\limits_{m=\frac{n+1}{2}}^{n-1}(2n+m)^{2}+(t-1)\times \sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3n-m-k)^{2}]+(t-1)\times \sum\limits_{m=n}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2n+m-k)^{2}]+\frac{t^{2}-2t+1}{2}\times \sum\limits_{m=1}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(3n-m-k)^{2}]+\frac{t^{2}-2t+1}{2}\times \sum\limits_{m=\frac{n+1}{2}}^{n-1}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2n+m-k)^{2}]+\frac{t^{2}+t}{2}\times \sum\limits_{m=0}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n}(3n-m-k)^{2}]+\frac{t^{2}+t}{2}\times \sum\limits_{m=\frac{n+1}{2}}^{n}[\sum\limits_{k\equiv 1(mod 2)}^{n}(2n+m-k)^{2}].\)
After simplification, we get,
\(M_{1}^{**}(G)=36n^{2}+\sum\limits_{m=1}^{\frac{n-1}{2}}(9n^{2}t+m^{2}t-6nmt-9n^{2}-m^{2}+6nm)+\sum\limits_{m=\frac{n+1}{2}}^{n-1}(4n^{2}t+m^{2}t+4nmt-4n^{2}-m^{2}-4nm)+\sum\limits_{m=0}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(9n^{2}t+m^{2}t+k^{2}t-6nmt+2mkt-6nkt-9n^{2}-m^{2}-k^{2}+6nm-2mk+6nk)]+\sum\limits_{m=n}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(4n^{2}t+m^{2}t+k^{2}t+4nmt-2mkt-4nkt-4n^{2}-m^{2}-k^{2}-4nm+2mk+4nk)]+\sum\limits_{m=1}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(\frac{9}{2}n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}-3nmt^{2}+mkt^{2}-3nkt^{2}-9n^{2}t-m^{2}t-k^{2}t+6nmt-2mkt+6nkt+\frac{9}{2}n^{2}+\frac{1}{2}m^{2}+\frac{1}{2}k^{2}-3nm+mk-3nk)]+\sum\limits_{m=\frac{n+1}{2}}^{n-1}[\sum\limits_{k\equiv 0(mod 2)}^{n-1}(2n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}+2nmt^{2}-mkt^{2}-2nkt^{2}-4n^{2}t-m^{2}t-k^{2}t-4nmt+2mkt+4nkt+2n^{2}+\frac{1}{2}m^{2}+\frac{1}{2}k^{2}+2nm-mk-2nk)]+\sum\limits_{m=0}^{\frac{n-1}{2}}[\sum\limits_{k\equiv 1(mod 2)}^{n}(\frac{9}{2}n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}-3nmt^{2}+mkt^{2}-3nkt^{2}+\frac{9}{2}n^{2}t+\frac{1}{2}m^{2}t+\frac{1}{2}k^{2}t-3nmt+mkt-3nkt)]+\sum\limits_{m=\frac{n+1}{2}}^{n}[\sum\limits_{k\equiv 1(mod 2)}^{n}(2n^{2}t^{2}+\frac{1}{2}m^{2}t^{2}+\frac{1}{2}k^{2}t^{2}+2nmt^{2}-mkt^{2}-2nkt^{2}+2n^{2}t+\frac{1}{2}m^{2}t+\frac{1}{2}k^{2}t+2nmt-mkt-2nkt)].\) ◻
Theorem 10. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 0(mod 2)\). The third Zagreb-eccentricity index is equal to,
\(M_{2}^{*}(G)=\sum\limits_{i=1}^{\frac{n}{2}}\sum\limits_{p=2n-\frac{n}{2}}^{2n-1}(6ip^{2}-3p^{2}+6ip-3p)+\sum\limits_{p=n\equiv 0(mod 2)}(12np^{2}+6np)+\sum\limits_{p=n\equiv 0(mod 2)}(8p^{2}+8p+2)+\sum\limits_{i=\frac{n}{2}+3}(\frac{n}{2}-1)\underbrace{times}(6i-16)\times \sum\limits_{p=2n+1}^{3n-\frac{n}{2}-1}(p^{2}+p)+\sum\limits_{i=3n+6j,0\leq j \leq \frac{n}{2}-1}\sum\limits_{p=3n-\frac{n}{2}}^{3n-1}(6np^{2}-ip^{2}+6np-ip).\)
Proof. Let \(G\cong NA^{n}_{m}\). From Eq. (6), we have, \[M_{2}^{*}(G)=\sum\limits_{uv\in E(G)}\epsilon(u).\epsilon(v).\]
By utilizing Table 3, we get,
\(M_{2}^{*}(G)=\sum\limits_{i=1}^{\frac{n}{2}}(6i-3)\times \sum\limits_{p=2n-\frac{n}{2}}^{2n-1}(p).(p+1)+\sum\limits_{p=n\equiv 0(mod 2)}3n\times (p).(2p+1)+\sum\limits_{p=n\equiv 0(mod 2)}2\times (2p+1).(2p+1)+\sum\limits_{i=\frac{n}{2}+3}(\frac{n}{2}-1)\underbrace{times}(6i-16)\times \sum\limits_{p=2n+1}^{3n-\frac{n}{2}-1}(p).(p+1)+\sum\limits_{i=3n+6j,0\leq j \leq \frac{n}{2}-1}(6n-i)\times \sum\limits_{p=3n-\frac{n}{2}}^{3n-1}(p).(p+1).\)
After simplification, we get
\(M_{2}^{*}(G)=\sum\limits_{i=1}^{\frac{n}{2}}\sum\limits_{p=2n-\frac{n}{2}}^{2n-1}(6ip^{2}-3p^{2}+6ip-3p)+\sum\limits_{p=n\equiv 0(mod 2)}(12np^{2}+6np)+\sum\limits_{p=n\equiv 0(mod 2)}(8p^{2}+8p+2)+\sum\limits_{i=\frac{n}{2}+3}(\frac{n}{2}-1)\underbrace{times}(6i-16)\times \sum\limits_{p=2n+1}^{3n-\frac{n}{2}-1}(p^{2}+p)+\sum\limits_{i=3n+6j,0\leq j \leq \frac{n}{2}-1}\sum\limits_{p=3n-\frac{n}{2}}^{3n-1}(6np^{2}-ip^{2}+6np-ip).\) ◻
| \([\epsilon_u,\epsilon_v]\) | \(\text{Range}\) | \(\text{Frequency}\) | \(\text{Range}\) |
| \([p,p+1]\) | \((2n-\frac{n}{2}\leq p \leq 2n-1)\) | \((3+6(i-1))\) | \((1\leq i \leq \frac{n}{2})\) |
| \([2p,2p+1]\) | \((p=n\equiv 0(mod 2))\) | \((3n)\) | \((n\equiv 0(mod 2))\) |
| \([2p+1,2p+1]\) | (\(p=n\equiv 0(mod 2))\) | \((2)\) | \((i=\frac{n}{2}+2)\) |
| \([p,p+1]\) | \((2n+1\leq p \leq 3n-\frac{n}{2}-1)\) | \(((\frac{n}{2}-1)\underbrace{times}[6i-16)])\) | \((i=\frac{n}{2}+3)\) |
| \([p,p+1]\) | \((3n-1 \geq p \geq 3n-\frac{n}{2})\) | \((6n-i)\) | \((i=3n+6j)\), |
| where | |||
| \((0\leq j \leq \frac{n}{2}-1)\). |
Theorem 11. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 1(mod 2)\). The third Zagreb-eccentricity index is,
\(M_{2}^{*}(G)=\sum\limits_{p=\frac{3n+1}{2}}(p^{2})+\sum\limits_{i=(\frac{n-1}{2})\underbrace{times} 2}\sum\limits_{p=\frac{3n+1}{2}}^{\frac{5n-1}{2},p\equiv 0(mod 2)}(ip^{2})+\sum\limits_{i\equiv 1(mod 2)}^{\frac{n-3}{2}}\sum\limits_{p=\frac{3n+1}{2}}^{2n-2,p\equiv 0(mod 2)}(4ip^{2}+4ip)+\sum\limits_{i\equiv 0(mod 2)}^{\frac{n-1}{2}}\sum\limits_{p=\frac{3n+3}{2}}^{2n-1,p\equiv 1(mod 2)}(8ip^{2}-2p^{2}+8ip-2p)+\sum\limits_{i=2n+2}(\frac{n+3}{4})\underbrace{times}i\times \sum\limits_{p=2n}^{\frac{5n-1}{2},p\equiv 0(mod 2)}(p^{2}+p)+\sum\limits_{i=4n}(\frac{n-1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-3}{2},p\equiv 1(mod 2)}(p^{2}+p)+\sum\limits_{i=\frac{n-1}{4}}^{1}16i\times \sum\limits_{p=\frac{5n+1}{2}}^{3n-2,p\equiv 1(mod 2)}(p^{2}+p)+\sum\limits_{i=\frac{n-3}{2}}^{1,i\equiv 1(mod 2)}4i\times \sum\limits_{p=\frac{5n+3}{2}}^{3n-1,p\equiv 0(mod 2)}(p^{2}+p).\)
Proof. Let \(G\cong NA^{n}_{m}\). From Eq. (6), we have \[M_{2}^{*}(G)=\sum\limits_{uv\in E(G)}\epsilon(u).\epsilon(v).\]
By utilizing Table 4, we get,
\(M_{2}^{*}(G)=1\times \sum\limits_{p=\frac{3n+1}{2}}(p).(p)+\sum\limits_{i=(\frac{n-1}{2})\underbrace{times} 2}i\times \sum\limits_{p=\frac{3n+1}{2}}^{\frac{5n-1}{2},p\equiv 0(mod 2)}(p).(p)+\sum\limits_{i\equiv 1(mod 2)}^{\frac{n-3}{2}}4i\times \sum\limits_{p=\frac{3n+1}{2}}^{2n-2,p\equiv 0(mod 2)}(p).(p+1)+\sum\limits_{i\equiv 0(mod 2)}^{\frac{n-1}{2}}(8i-2)\times \sum\limits_{p=\frac{3n+3}{2}}^{2n-1,p\equiv 1(mod 2)}\\(p).(p+1)+\sum\limits_{i=2n+2}(\frac{n+3}{4})\underbrace{times}i\times \sum\limits_{p=2n}^{\frac{5n-1}{2},p\equiv 0(mod 2)}(p).(p+1)+\sum\limits_{i=4n}(\frac{n-1}{4})\underbrace{times}\\i\times \sum\limits_{p=2n+1}^{\frac{5n-3}{2},p\equiv 1(mod 2)}(p).(p+1)+\sum\limits_{i=\frac{n-1}{4}}^{1}16i\times \sum\limits_{p=\frac{5n+1}{2}}^{3n-2,p\equiv 1(mod 2)}(p).(p+1)+\sum\limits_{i=\frac{n-3}{2}}^{1,i\equiv 1(mod 2)}4i\times \sum\limits_{p=\frac{5n+3}{2}}^{3n-1,p\equiv 0(mod 2)}(p).(p+1).\)
After simplification, we get,
\(M_{2}^{*}(G)=\sum\limits_{p=\frac{3n+1}{2}}(p^{2})+\sum\limits_{i=(\frac{n-1}{2})\underbrace{times} 2}\sum\limits_{p=\frac{3n+1}{2}}^{\frac{5n-1}{2},p\equiv 0(mod 2)}(ip^{2})+\sum\limits_{i\equiv 1(mod 2)}^{\frac{n-3}{2}}\sum\limits_{p=\frac{3n+1}{2}}^{2n-2,p\equiv 0(mod 2)}(4ip^{2}+4ip)+\sum\limits_{i\equiv 0(mod 2)}^{\frac{n-1}{2}}\sum\limits_{p=\frac{3n+3}{2}}^{2n-1,p\equiv 1(mod 2)}\) \((8ip^{2}-2p^{2}+8ip-2p)+\sum\limits_{i=2n+2}(\frac{n+3}{4})\underbrace{times}i\times \sum\limits_{p=2n}^{\frac{5n-1}{2},p\equiv 0(mod 2)}(p^{2}+p)+\sum\limits_{i=4n}(\frac{n-1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-3}{2},p\equiv 1(mod 2)}(p^{2}+p)+\sum\limits_{i=\frac{n-1}{4}}^{1}16i\times \sum\limits_{p=\frac{5n+1}{2}}^{3n-2,p\equiv 1(mod 2)}(p^{2}+p)+\sum\limits_{i=\frac{n-3}{2}}^{1,i\equiv 1(mod 2)}4i\times \sum\limits_{p=\frac{5n+3}{2}}^{3n-1,p\equiv 0(mod 2)}(p^{2}+p).\) ◻
| \([\epsilon_u,\epsilon_v]\) | \(\text{Range}\) | \(\text{Frequency}\) | \(\text{Range}\) |
| \([p,p]\) | \(\lbrace p=\frac{3n+1}{2}\rbrace\) | \(\lbrace 1\rbrace\) | |
| \([p,p]\) | \((\frac{5n-1}{2}\geq p \geq \frac{3n+1}{2})\), \(p\) is even | \(\lbrace i\rbrace\) | \(\lbrace i=(\frac{n-1}{2})\underbrace{times}2\rbrace\) |
| \([p, p+1]\) | \((3n-1\geq p \geq \frac{5n+3}{2})\), \(p\) is even | \(\lbrace 4i\rbrace\) | \((1\geq i \geq \frac{n-3}{2}), \lbrace i\equiv 1(mod 2)\rbrace\) |
| \([p, p+1]\) | \((2n-1 \geq p \geq \frac{3n+3}{2})\), \(p\) is even | \(\lbrace 8i-2\rbrace\) | \((\frac{n-1}{2}\geq i \geq 2) , \lbrace i\equiv 0(mod 2)\rbrace\) |
| \([p, p+1]\) | \((\frac{5n-1}{2}\geq p \geq 2n)\), \(p\) is even | \(\lbrace i=2n+2\rbrace\) | \(\lbrace (\frac{n+3}{4})\underbrace{times}i\rbrace\) |
| \([p, p+1]\) | \((\frac{5n-3}{2}\geq p \geq 2n+1)\), \(p\) is odd | \(\lbrace i=4n\rbrace\) | \(\lbrace (\frac{n-1}{4})\underbrace{times}i\rbrace\) |
| \([p, p+1]\) | \((3n-2\geq p \geq \frac{5n+1}{2})\), \(p\) is odd | \(\lbrace 16i\rbrace\) | \((1\geq i \geq \frac{n-1}{4})\) |
| \([p, p+1]\) | \((2n-2 \geq p \geq \frac{3n+1}{2})\), \(p\) is even | \(\lbrace 4i\rbrace\) | \((\frac{n-3}{2}\geq i \geq 1)\), \(i\) is even |
| \([\epsilon_u,\epsilon_v]\) | \(\text{Range}\) | \(\text{Frequency}\) | \(\text{Range}\) |
| \([p,p]\) | \((\frac{3n+3}{2}\leq p \leq \frac{5n+1}{2})\) | \(\lbrace i\rbrace\) | \(\lbrace i=(\frac{n+1}{2})\underbrace{times}2\rbrace\) |
| \([p,p+1]\) | \((\frac{3n+1}{2}\leq p \leq 2n-1)\), \( p\) is odd | \(\lbrace 16i-10\rbrace\) | \((1\leq i \leq \frac{n+1}{4})\) |
| \([p,p+1]\) | \((\frac{3n+3}{2}\leq p \leq 2n)\), \( p\) is even | \(\lbrace 8i\rbrace\) | \((1\leq i \leq \frac{n+1}{4})\) |
| \([p,p+1]\) | \((2n+1 \leq p \leq \frac{5n-1}{2})\), \( p\) is odd | \(\lbrace i=4n\rbrace\) | \(\lbrace (\frac{n+1}{4})\underbrace{times}i\rbrace\) |
| \([p,p+1]\) | \((\frac{5n-3}{2}\geq p \geq 2n+2)\), \( p\) is even, \(n\neq 3\) | \(\lbrace i=2n+2\rbrace, n\neq 3\) | \(\lbrace (\frac{n-3}{4})\underbrace{times}i\rbrace, n\neq 3\) |
| \([p,p+1]\) | \((3n-2\geq p \geq \frac{5n+3}{2})\), \( p\) is odd \(, \)n 3\(\) | \(\lbrace 16i\rbrace\) | \((\frac{n-3}{4}\leq i \leq 1), n\neq 3\) |
| \([p,p+1]\) | \((3n-1\geq p \geq \frac{5n+1}{2})\), \( p\) is even\(\) | \(\lbrace 8i-4\rbrace\) | \((\frac{n+1}{4}\leq i \leq 1)\) |
Theorem 12. Let \(G\cong NA^{n}_{m}\) with \(n\equiv 3(mod 4)\). The third Zagreb-eccentricity index is,
\(M_{2}^{*}(G)=\sum\limits_{i=(\frac{n+1}{2})\underbrace{times}2}\sum\limits_{p=\frac{3n+3}{2}}^{\frac{5n+1}{2},p\equiv 0(mod 2)}(ip^{2})+\sum\limits_{i=1}^{\frac{n+1}{4}}\sum\limits_{\frac{3n+1}{2}}^{2n-1,p\equiv 1(mod 2)}\\(16ip^{2}-10p^{2}+16ip-10p)+\sum\limits_{i=1}^{\frac{n+1}{4}}\sum\limits_{p=\frac{3n+3}{2}}^{2n,p\equiv 0(mod 2)}(8ip^{2}+8ip)+\sum\limits_{i=4n}(\frac{n+1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-1}{2},p\equiv 1(mod 2)}(p^{2}+p)+\sum\limits_{i=2n+2,n\neq 3}(\frac{n-3}{4})\underbrace{times}i\times \sum\limits_{p=2n+2,n\neq 3}^{\frac{5n-3}{2},p\equiv 0(mod 2)}(p^{2}+p)+\sum\limits_{i=\frac{n-3}{4}}^{1,n\neq 3}\sum\limits_{p=\frac{5n+3}{2},n\neq 3}^{3n-2,p\equiv 1(mod 2)}(16ip^{2}+16ip)+\sum\limits_{i=\frac{n+1}{4}}^{1}\sum\limits_{p=\frac{5n+1}{2}}^{3n-1,p\equiv 0(mod 2)}(8ip^{2}-4p^{2}+8ip-4p).\)
Proof. Let \(G\cong NA^{n}_{m}\). From Eq. (6), we have, \[M_{2}^{*}(G)=\sum\limits_{uv\in E(G)}\epsilon(u).\epsilon(v).\]
By utilizing Table 5, we get,
\(M_{2}^{*}(G)=\sum\limits_{i=(\frac{n+1}{2})\underbrace{times}2}i\times \sum\limits_{p=\frac{3n+3}{2}}^{\frac{5n+1}{2},p\equiv 0(mod 2)}(p).(p)+\sum\limits_{i=1}^{\frac{n+1}{4}}(16i-10)\times \sum\limits_{\frac{3n+1}{2}}^{2n-1,p\equiv 1(mod 2)}(p).(p+1)+\sum\limits_{i=1}^{\frac{n+1}{4}}8i\times \sum\limits_{p=\frac{3n+3}{2}}^{2n,p\equiv 0(mod 2)}(p).(p+1)+\sum\limits_{i=4n}(\frac{n+1}{4})\\\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-1}{2},p\equiv 1(mod 2)}(p).(p+1)+\sum\limits_{i=2n+2,n\neq 3}(\frac{n-3}{4})\underbrace{times}i\times \sum\limits_{p=2n+2,n\neq 3}^{\frac{5n-3}{2},p\equiv 0(mod 2)}\\(p).(p+1)+\sum\limits_{i=\frac{n-3}{4}}^{1,n\neq 3}16i\times \sum\limits_{p=\frac{5n+3}{2},n\neq 3}^{3n-2,p\equiv 1(mod 2)}(p^{2}+p)+\sum\limits_{i=\frac{n+1}{4}}^{1}(8i-4)\times \sum\limits_{p=\frac{5n+1}{2}}^{3n-1,p\equiv 0(mod 2)}\\(p).(p+1).\)
After simplification, we get,
\(M_{2}^{*}(G)=\sum\limits_{i=(\frac{n+1}{2})\underbrace{times}2}\sum\limits_{p=\frac{3n+3}{2}}^{\frac{5n+1}{2},p\equiv 0(mod 2)}(ip^{2})+\sum\limits_{i=1}^{\frac{n+1}{4}}\sum\limits_{\frac{3n+1}{2}}^{2n-1,p\equiv 1(mod 2)}(16ip^{2}-10p^{2}+16ip-10p)+\sum\limits_{i=1}^{\frac{n+1}{4}}\sum\limits_{p=\frac{3n+3}{2}}^{2n,p\equiv 0(mod 2)}(8ip^{2}+8ip)+\sum\limits_{i=4n}(\frac{n+1}{4})\underbrace{times}i\times \sum\limits_{p=2n+1}^{\frac{5n-1}{2},p\equiv 1(mod 2)}(p^{2}+p)+\sum\limits_{i=2n+2,n\neq 3}(\frac{n-3}{4})\underbrace{times}i\times \sum\limits_{p=2n+2,n\neq 3}^{\frac{5n-3}{2},p\equiv 0(mod 2)}(p^{2}+p)+\sum\limits_{i=\frac{n-3}{4}}^{1,n\neq 3}\sum\limits_{p=\frac{5n+3}{2},n\neq 3}^{3n-2,p\equiv 1(mod 2)}(16ip^{2}+16ip)+\sum\limits_{i=\frac{n+1}{4}}^{1}\sum\limits_{p=\frac{5n+1}{2}}^{3n-1,p\equiv 0(mod 2)}(8ip^{2}-4p^{2}+8ip-4p).\) ◻
In this paper we considered the chemical graph of \(G\cong NA^{n}_{m}\) and computed eccentric connectivity index with total eccentricity index and some versions of the zagreb indices which are the most prominent eccentricity based graph invariants in chemical graph theory. The results are valid and useful for the modeling of biological activities.
This declaration is not applicable.
There is no scientific or financial conflict of interests between the authors and we feel convenient to submit.
The author Wasim Sajjad conducted this research under the supervision of Prof. Xiang-Feng Pan and concluded the results. M. Shoaib Sardar verified the main results of the research article and reviewed it.
This declaration is not applicable.
All relevant data is given in the manuscript, there is no hidden or unpublished data.
Durgi, B. S., Mekkalike, S. M., & Hosamani, S. M. (2020). Applications of Eccentricity based Topological Indices in QSPR studies. Journal of Xi’an University of Architecture and Technology, 12(4), 5691-5705.
Guo, D., Tao, D., Siddiqui, M. K., Naeem, M., Baig, A. Q., & Azhar, M. R. (2020). ECCENTRICITY BASED TOPOLOGICAL INDICES OF CHAIN OCTAHEDRON STRUCTURE. Revue Roumaine de Chimie, 65(5), 433-445.
West, D. B. (2001). Introduction to Graph Theory (Vol. 2). Upper Saddle River: Prentice hall.
Shaker, H., Imran, M., & Sajjad, W. (2021). Eccentricity based topological indices of face centered cubic lattice FCC (n). Main Group Metal Chemistry, 44(1), 32-38.
Tang, Y., & Qi, X. (2021). Ordering graphs with large eccentricity-based topological indices. Journal of Inequalities and Applications, 2021(1), 24.
Gutman, I., & Trinajstić, N. (1972). Graph theory and molecular orbitals. Total \(\phi\)-electron energy of alternant hydrocarbons. Chemical physics letters, 17(4), 535-538.
Huo, Y., Liu, J. B., Baig, A. Q., Sajjad, W., & Farahani, M. R. (2017). Connective Eccentric Index of NA nm Nanotube. Journal of Computational and Theoretical Nanoscience, 14(4), 1832-1836.
Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69(1), 17-20.
Ramane, H. S., & Yalnaik, A. S. (2017). Status connectivity indices of graphs and its applications to the boiling point of benzenoid hydrocarbons. Journal of Applied Mathematics and Computing, 55, 609-627.
Sharma, V., Goswami, R., & Madan, A. K. (1997). Eccentric connectivity index: A novel highly discriminating topological descriptor for structure-property and structure-activity studies. Journal of Chemical Information and Computer Sciences, 37(2), 273-282.
Ilic, A., & Gutman, I. (2011). Eccentric connectivity index of chemical trees. MATCH Communications in Mathematical and in Computer Chemistry, 65(3), 731–744.
De, N., Abu Nayeem, S. M., & Pal, A. (2015). Total eccentricity index of the generalized hierarchical product of graphs. International Journal of Applied and Computational Mathematics, 1, 503-511.
Fathalikhani, K., Faramarzi, H., & Yousefi-Azari, H. (2014). Total eccentricity of some graph operations. Electronic Notes in Discrete Mathematics, 45, 125-131.
Zaman, S., & Ali, A. (2021). On connected graphs having the maximum connective eccentricity index. Journal of Applied Mathematics and Computing, 67, 131-142.
Indices, S. N. Z. E. (2010). Note on the comparison of the first and second normalized Zagreb eccentricity indices. Acta Chimica Slovenica, 57, 524-528.
Ghorbani, M., & Hosseinzadeh, M. A. (2012). A new version of Zagreb indices. Filomat, 26(1), 93-100.
Wang, H., Hua, H., & Wang, M. (2020). Comparative study of distance-based graph invariants. Journal of Applied Mathematics and Computing, 64, 457-469.
Gao, F., Zhao, D. D., Li, X. X., & Liu, J. B. (2018). Graphs having extremal monotonic topological indices with bounded vertex k-partiteness. Journal of Applied Mathematics and Computing, 58, 413-432.
Luo, Z., & Wu, J. (2014). Zagreb eccentricity indices of the generalized hierarchical product graphs and their applications. Journal of Applied Mathematics, 2014(1), 241712.
Qi, X., Zhou, B., & Li, J. (2017). Zagreb eccentricity indices of unicyclic graphs. Discrete Applied Mathematics, 233, 166-174.
Liu, J. B., Gu, J. J., & Wang, K. (2023). The expected values for the Gutman index, Schultz index, and some Sombor indices of a random cyclooctane chain. International Journal of Quantum Chemistry, 123(3), e27022.