
The development of chatbot systems for mathematics courses in elementary school has gained significant attention due to their potential to enhance the learning experience. This study proposes a novel approach that combines knowledge graph (KG) and Named Entity Recognition (NER) methods using Neo4j and SpaCy within the Rasa Open-Source v3.0 platform as chatbot frameworks. The knowledge graphs represent mathematical concepts and their relationships, enabling the chatbot to provide accurate and relevant responses to user queries. The NER SpaCy is employed to identify and extract mathematical entities from user inputs, ensuring a precise understanding of the context. The integrations of Neo4j and NER using SpaCy with Rasa Open-Source v3.0 facilitate efficient information retrieval and improve the conversational abilities of the chatbot. Experimental results demonstrate the effectiveness of the proposed approach, showcasing its potential as an educational tool for fifth-grade students in elementary schools.
Copyright © 2024 Hasna Salsabila and Isnaini Rosyida. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
In recent years, there has been a growing interest in developing intelligent chatbot systems to enhance the learning experience in various domains, including mathematics education. These chatbots provide private and interactive conversations that allow students to engage in a dynamic learning process. One crucial aspect of developing a chatbot is the extraction and organization of relevant information. Labadze et al. discussed the benefits of AI chatbots in education [1]. Memon et al. constructed an educational domain-based multichatbot communication system [2]. Further, Okonkwo and Ade-Ibijola also provided chatbot applications in education [3].
A knowledge graph (KG) is a powerful representation of structured data that captures relationships and connections among different entities. It provides efficient storage and retrieval of information, making it ideal for building intelligent chatbot systems [4]. Patsoulis et al. provided chatbot integration with knowledge graphs in e-government [5]. Timon-Reina et al. proposed graph databases and their implementations in the biomedical fields [6]. Moreover, Zou described some applications of the KG [7]. Yoo and Jeong constructed an intelligent chatbot using the BERT model and KG [8]. Agrawal et al. built KG from unstructured texts and implemented it in cybersecurity education [9]. Xue provided life-long education data classification based on a KG [10]. Meloni et al. integrated conversational agents with KG focused on the scholarly domain [11]. Buhl et al. designed a chatbot based on KG that actively learned from humans [12]. Moreover, Nair and Shivani proposed a question-answering model using KG for remote school education [13].
On the other hand, Named Entity Recognition (NER) is a Natural Language Processing (NLP) technique that identifies and categorizes named entities, such as names of people, places, organizations, and numerical expressions, in a text document [14]. Khairunnisa et al. discussed dataset enhancement and multilingual transfer for NER in the Indonesian language [15]. Yanti et al. proposed an application of NER via Twitter on SpaCy in Indonesian [16]. Ali designed a chatbot with the NER model using an artificial neural network [17]. Therefore, knowledge graphs and NER techniques play a significant role in constructing a chatbot system.
In this article, we construct a chatbot system for fifth-grade elementary school mathematics using Rasa Open Source v3.0 as the chatbot framework. The system incorporates the utilization of knowledge graphs and NER techniques through Neo4j and SpaCy libraries, respectively. By leveraging these tools, the chatbot system aims to provide contextually relevant responses to student queries so that it enhances their learning experience.
This paper is organized into five sections. The second section is preliminaries. The third section discusses the method used in this research. The fourth part provides results and discussion. Finally, the conclusions are given in the fifth section.
The next subsections provide some basic concepts used in this paper.
NER is a significant task in Natural Language Processing (NLP). The NER can be defined as a method for information extraction that processes both structured and unstructured documents to identify entities such as people, locations, organizations, or companies. The term “named entity” was first introduced as a crucial component of information extraction at the Sixth Message Understanding Conference (MUC-6) [18]. The MUC-6 categorized named entities into three label types: ENAMEX (people, organizations, locations), TIMEX (dates and times), and NUMEX (money, percentages, quantities) [19].
A graph G=(V, E) consists of a node-set V and an edge set E, where each edge indicates a connection between two nodes in the graph. Whereas a knowledge graph (KG), often called a semantic network, illustrates the connections among real-world elements, including concepts, events, objects, and circumstances, as well as the network of these connections. The term KG was coined since this information is commonly stored in a graph database and portrayed as a graph structure. The three primary parts of a KG are labels, edges, and nodes. A node can be any item, location, or person. The relationship between the nodes is defined by an edge. A customer like IBM or an agency like Ogilvy are two examples of nodes. An edge would be a customer relationship between IBM and Ogilvy [20].
A KG can also be represented in three triples, i.e., head (h), tail (t), and predicate (p), where h and t are elements of V, that indicate subject and object (entities), and p is an element of E that describes a semantic relationship between the subject and object ([21], [22]). For instance, Figure 1 shows a KG with three triples (h, t, and p) as follows: square (“persegi”), triangle (“segitiga”), and trapezoid (“trapesium”) are objects, two-dimensional shape (“bangun datar”) is the subject, and the predicate (p) is “belongs to.” Further, a triangle is also a subject and a square is an object with the relation “contained in,” etc.
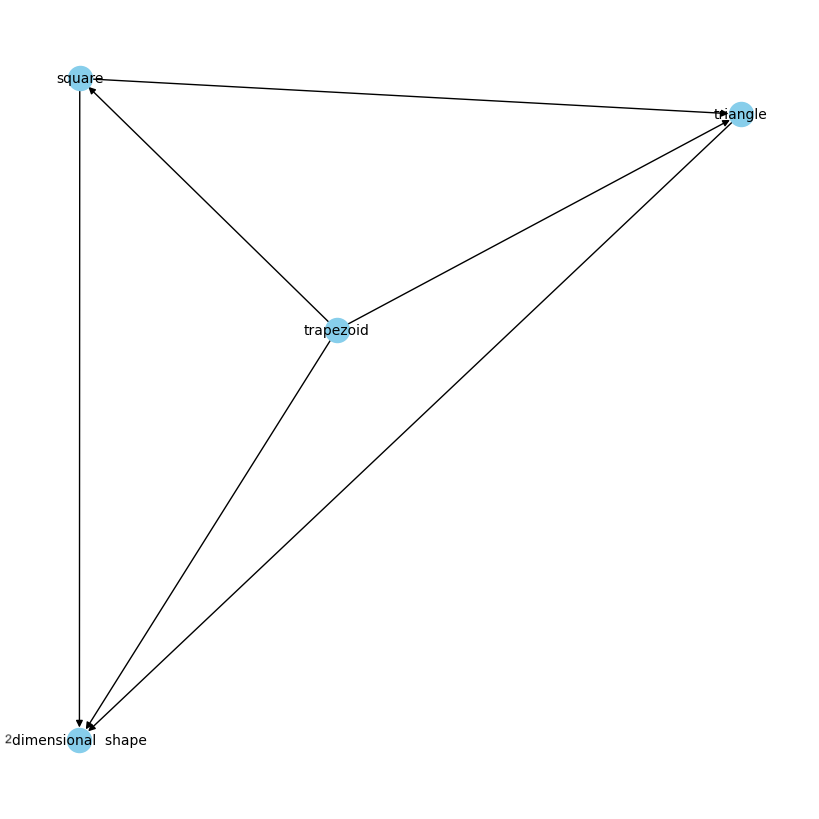
In 2012, Google introduced the KG, used as semantic knowledge in search. The function of the Google KG is to identify entities in the text to enhance search results by providing semantically structured summaries and links to connect entities in research queries [23]. This search aims to improve search engines and user research experiences. The most common applications of the KG are in question-answering systems, recommender systems, and information retrieval. In chatbots, a KG is usually built upon existing modules to connect all gathered information, bridging structured and unstructured information, and representing this information in a clear and structured form to users [24]. Another example of the usage of KG is in Kbot to select responses and provide feedback to the user. User queries result in named entities, and information from these entities is extracted using NER. The extracted results from these entities using NER are used to construct a KG. For example, in Kbot, a user’s question “Who is Alan Turing?” would be categorized as “person” using NER, and “Alan Turing” would be extracted as the main entity [25].
An open-source machine learning framework called Rasa is used to create chatbots and AI agents. It is an open-source library that provides a framework for creating Python-based programming language chatbots [26]. Rasa consists of two components, i.e., Rasa Natural Language Understanding (NLU) and Rasa Core. Both components have their respective roles in the chatbot system. In the latest version, they merged into one system called Rasa. On the one hand, Rasa NLU is utilized to interpret messages sent by users. On the other hand, conversations and decision-making are handled by Rasa Core [27]. Various researchers have developed chatbots using the Rasa framework, such as in ([28], [29]). Rasa’s most recent release is called Rasa X, which is a tool that supports the creation, enhancement, and implementation of AI assistants driven by the Rasa framework. Rasa NLU has some additional features, i.e., SpaCy and tensorflow. The Spacy is a free and open-source package for advanced NLP in Python.
The methods used to construct the chatbot are as follows.
Using KG and NER methods, along with Neo4j and SpaCy library, to build a chatbot system for the mathematics course in the fifth-grade elementary school with Rasa Open Source v3.0 as the chatbot framework, showed promising results. In this section, we present the outcomes of our experiments and discuss their implications.
The KG plays a crucial role in organizing and representing the domain-specific knowledge required for the chatbot. Neo4j, a graph database, creates and manages the KG efficiently. We extract mathematical concepts and their relationships from various sources, such as textbooks, online educational materials, and curriculum guidelines. These entities are modeled as nodes in the graph, while their relationships are represented as edges. The KG provides a structured representation of the mathematical knowledge, allowing the chatbot to access and utilize it effectively. The KG in Neo4j is depicted in Figure 1. Meanwhile, the graph database in Neo4j is shown in Figure 3.
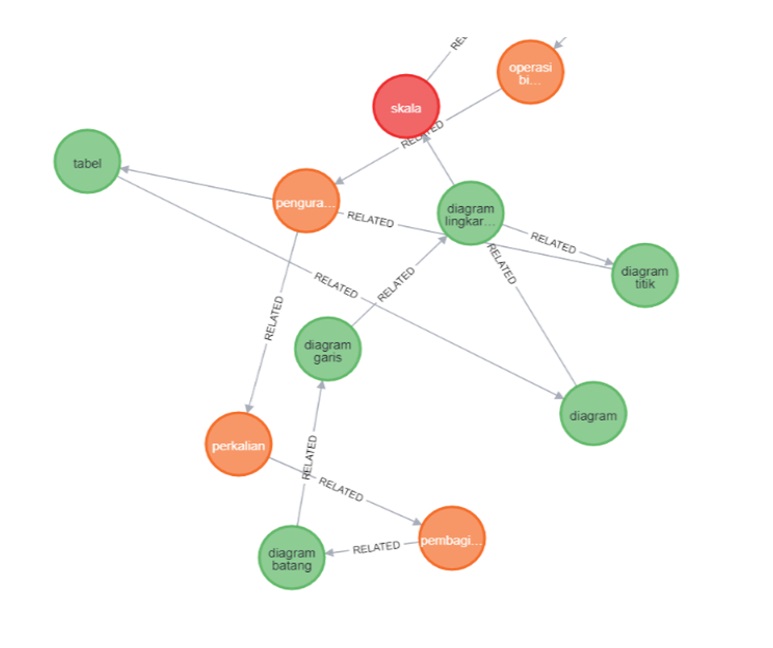

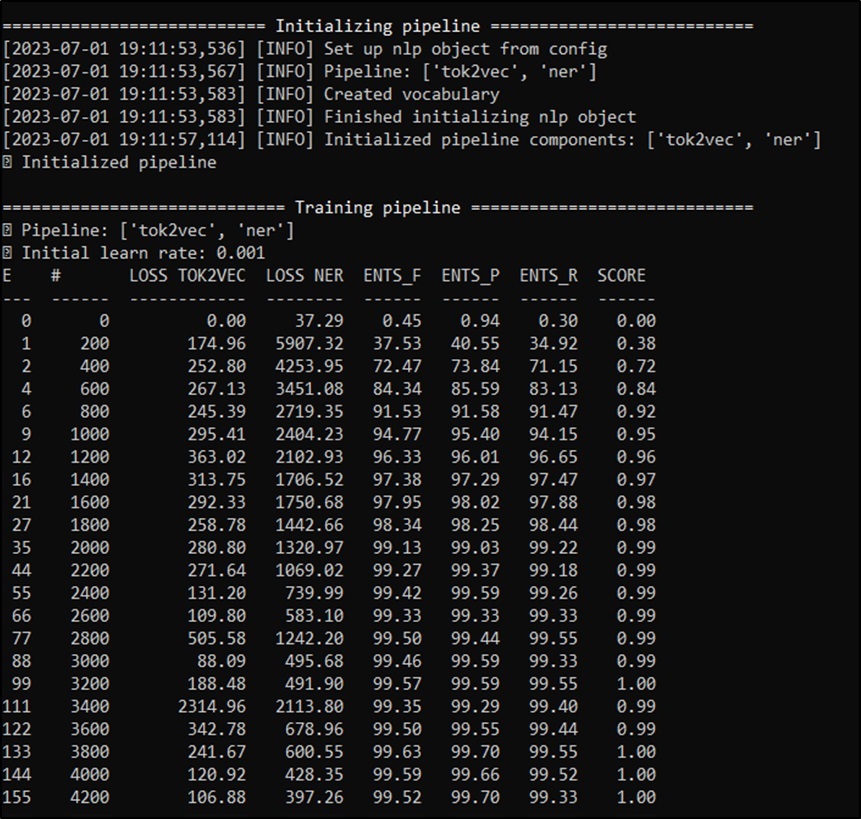
Furthermore, we employ NER with SpaCy to identify relevant entities within user queries. The NER model is trained on a dataset containing annotated examples of mathematical entities such as numbers, operations, units of measurement, and mathematical terms. By incorporating NER, the chatbot could accurately recognize and extract mathematical entities from user input, enabling it to provide more precise and contextually appropriate responses. The training process is described in Figure 4.
We have seen notable improvements in the chatbot’s performance after conducting thorough testing and evaluation. The chatbot’s capacity to comprehend and analyze mathematical queries is improved by the combination of the KG and NER approaches. The chatbot could accurately identify mathematical entities mentioned in user queries, enabling it to retrieve relevant information from the KG. This resulted in more accurate and informative responses provided by the chatbot. The appearance of NER with SpaCy using displaCy is shown in Figure 5. DisplaCy is the quickest tool to visualize named entities.
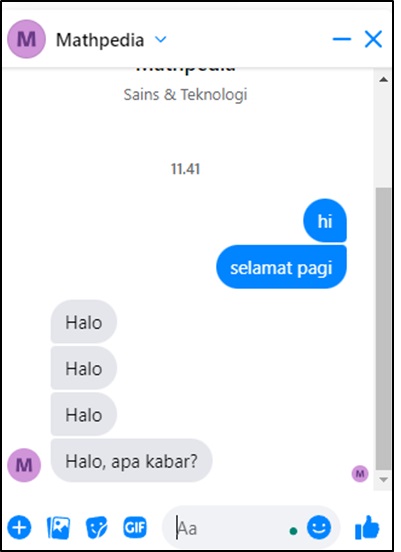
Moreover, the chatbot’s utilization of the KG facilitates intelligent responses based on the relationships among mathematical concepts. It could provide explanations, examples, and step-by-step solutions by traversing the graph and retrieving connected nodes and edges. This feature proves to be highly beneficial for students, as it enhances their understanding of mathematical concepts and problem-solving techniques. The chatbot implementation result is given in Figure 6.

Overall, the integration of the KG and NER methods using Neo4j and SpaCy in the development of the chatbot system yields promising results. The chatbot demonstrates improved accuracy and effectiveness in understanding and responding to mathematical queries from fifth-grade elementary school students. The combination of Rasa open-source v3.0 as the chatbot framework, along with these methods, showcases the potential for developing an intelligent chatbot system in the field of mathematics education.
Following the outcome, it was clear that using the Rasa Framework, the Named Entity Recognition (NER) method, and knowledge graphs (KG) to build a conversation system in a mathematics chatbot was a successful method that made it easier for users to interact with the chatbot. Through the implementation of the Rasa framework, the chatbot could provide a more natural and responsive conversational experience. The use of the NER method in extracting information from text related to mathematics subject matter and user queries in the chatbot has proven capable of identifying and extracting important entities such as mathematical concepts, formulas, variables, and other related keywords. This enables the chatbot to understand and respond more accurately and relevantly to user queries. As a knowledge base for the chatbot, using the KG as a model and visualization of subject matter entities that students often talk about was very helpful because it gave structured and logically connected information. The KG allowed the chatbot to provide deeper and more detailed explanations of mathematical concepts as well as display relationships between these concepts. With the presence of the KG, the chatbot could provide more comprehensive answers and assist users in understanding mathematics subject matter.
Based on the results of this research, several suggestions could be given for the development of a conversation system in a mathematics chatbot using KG and NER, as follows: expanding the range of recognized entities in the system to enhance the quality and accuracy of entity recognition. Further development is needed to identify and extract more specific mathematical entities. To accomplish this, it is necessary to use more pertinent sources and datasets, create more intricate conversational interactions for responding to user inquiries, and improve the chatbot to interact with users by asking follow-up questions, offering practice problems, or presenting case studies.
Further, it is important to evaluate and improve the chatbot system continuously. Collecting feedback from users and regularly monitoring the chatbot’s performance can help identify weaknesses and address existing shortcomings. Integration with other platforms and services to enhance accessibility and chatbot utilization should be reconsidered, especially integration with frequently used platforms or services such as instant messaging applications or online learning platforms. This can enhance the utilization of the chatbot in the field of education. It is expected that the development of a conversation system in a mathematics chatbot using KG and NER could be continuously improved since it will provide greater benefits in supporting interactive and effective mathematics learning.